Аналогичным образом представляем вектор градиента давления

grad P= 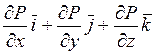(2.3)

Тогда выражение (2.2) можно представить

`V = 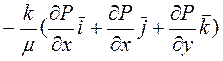. (б)

Сравнивая выражения (а) и (б), получаем

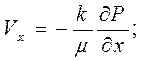
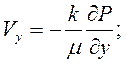
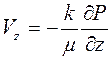. (2.4)

Уравнения (2.4), определяющие выражения для скоростей фильтрации флюида по закону Дарси в направлении координатных осей, называются уравнениями движения флюида.

Заметим, что в уравнениях (2.4) под давлением Р имеется в виду приведенное давление Р*=Р + gZ, где Р- давление пьезометрическое.

Для горизонтального пласта в уравнениях (2.4) давление Р есть давление пьезометрическое.

Перепишем уравнения (2.4) через пьзометрическое давление Р с учетом влияния силы тяжести, что имеет место при фильтрации в наклонных пластах.

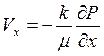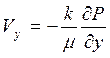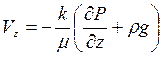; ; , (2.5)

где ось Z - направлена вертикально вверх .

В теории фильтрации оказывается удобным ввести функцию Ф(x,y,z,), называемую потенциалом скорости фильтрации и определяемую выражением:

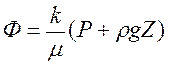. (2.6)

Тогда уравнения движения (2.5) с учетом (2.6) запишутся в виде:

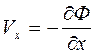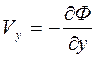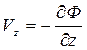, , . (2.7)

Таким образом, потенциаломскорости фильтрации называется функция Ф(x,y,z,), производная которой с обратным знаком вдоль линии тока равна скорости фильтрации V (x,y,z,).

С учетом (2.6) вектор скорости фильтрации (2.2) принимает вид:

`V = -grad Ф (2.8)

Выражения (2.7) и (2.8) представляют наиболее общую форму выражения линейного закона фильтрации и учитывают влияние силы тяжести на фильтрацию.