Базові поняття векторної графіки
Програмні засоби для роботи з векторною графікою призначені, в першу чергу, для створення ілюстрацій і меншою ступінню для їх обробки.
Принципи векторної графіки базуються на відмінному від піксельної графіки математичному апараті і мають метою побудувати лінійні контури, складені з елементарних кривих, які описуються математичними рівняннями.
Векторна графіка – це вид комп’ютерної графіки, в якому зображення подається у вигляді сукупності окремих об’єктів, описаних математично.
У растровій графіці основним елементом зображення є точка, а у векторній графіці - лінія (при цьому не важливо, пряма це лінія чи крива).
Звичайно, в растровій графіці теж існують лінії, проте там вони розглядаються як комбінації точок. Для кожної точки лінії в растровій графіці відводиться одна чи декілька комірок пам’яті (чим більше кольорів можуть мати точки, тим більше комірок їм виділяється). Відповідно, чим довша растрова лінія, тим більше пам’яті вона займає. У векторній графіці об’єм пам’яті, який займає лінія, не ї графіки їх розмір, форму і колір, але це не відіб’ється на якості їх віртуального уявлення. Векторна графіка не залежить від роздільної здатності, тобто може бути показана в різноманітних вихідних пристосуваннях із різною роздільною здатністю без втрати якості.
Векторний формат більш компактний, проте він зовсім непридатний для збереження фотографічних зображень. У цьому форматі задавати їх математично було б дуже громіздко. А ось рисунки і креслення значно зручніше і практичніше зробити саме в векторному вигляді.
Основними перевагами векторної графіки є:
1) зміна масштабу без втрати якості і практично без збільшення розмірів вихідного файлу,
2) велика точність (до сотої частки мікрона),
3) невеликий розмір файлу в порівнянні з растровими зображеннями,
4) висока якість друку,
5) відсутність проблем із експортом векторного зображення в растрове,
6) можливість редагування кожного елемента зображення окремо.
Основними недоліками векторної графіки є такі:
1) складність експорту з растрового в векторний формат,
2) неможливість застосування численної бібліотеки ефектів, які застосовуються під час роботи з растровими зображеннями.
Математичні основи векторної графіки
В основі векторної графіки лежать математичні уявлення про властивості геометричних фігур. Оскільки, найпростішим об’єктом векторної графіки є лінія, то в основі векторної графіки лежить, перш за все, математичне уявлення лінії.
Точка на площині задається двома числами (х,у), які визначаючають її положення відносно початку координат.
Для задання прямої лінії достатньо двох параметрів. Звично графік прямої лінії описується рівнянням у = kx + b. Знаючи параметри k і b, завжди можна зобразити безкінечну пряму лінію у відомій системі координат.
До кривих другого порядку відносяться: параболи, гіперболи, еліпси, кола і інші лінії, рівняння яких не містять ступенів вище другого.
Відрізняються криві другого порядку тим, що не мають точок перегину. Загальна формула кривої другого порядку може виглядати, наприклад, так:
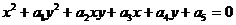 (2.1)
(2.1)
П’яти параметрів достатньо для опису безкінечної кривої другого порядку.
Відмінною особливістю кривої третього порядку є те, що вони можуть мати точку перегину.
Криві третього порядку добре відповідають тим лініям, які ми можемо бачити в живій природі, наприклад, лініям вигину людського тіла, тому в якості основних об’єктів векторної графіки застосовують саме такі лінії. Всі прямі і криві другого порядку (наприклад, коло чи еліпс) є окремими випадками кривих третього порядку.
У загальному випадку рівняння кривої третього порядку можна записати так:
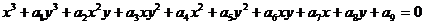 (2.2)
(2.2)
Із рівняння видно, що для запису кривої третього порядку достатньо дев’яти параметрів і зображення кривої третього порядку здійснюється за заданими коефіцієнтами її рівняння. Для спрощення цієї процедури в векторних редакторах застосовують не будь-які криві третього порядку, а їх особливий вид, названий кривими Безьє.
Питання про побудову апроксимуючого багаточлена привернув увагу багатьох математиків. Видатний вчений Сергій Натанович Бернштейн на початку ХХ століття запропонував доведення теореми Вейєрштрасса за допомогою теорії ймовірності. У цьому випадку необхідний поліном будується в явному вигляді (не параметрично). Саме даний поліном і став основою сплайнових кривих, зокрема NURBS-кривих і кривих Безьє.
Відрізки кривих Безьє – це окремий випадок відрізків кривих третього порядку. Вони описуються не одинадцятьма параметрами, як довільні відрізки кривих третього порядку, а лише вісьмома, і тому працювати з ними зручніше.
Метод побудови кривих Безьє базується на застосуванні пари дотичних проведених до лінії в точках її закінчення (рис. ).
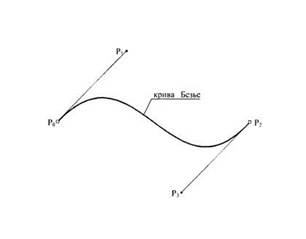
Рис. 1. Канонічний вид кривої Безьє
Для побудови кривої потрібно чотири контрольні точки. Проте крива фізично проходить тільки через дві з них, вони отримали назву опорних. Одна з цих точок називається початковою (start point), а інша – кінцевою (end point). Дві точки залишаються в стороні, вони отримали назву керуючих (control point). Для того, щоб їх не «втратити», в програмах векторної графіки керуючі точки з’єднуються з опорними точками лінією.
Для того щоб отримати величезну різноманітність форм, із яких можна скласти об’єкт будь-якої складності потрібно змінити форму канонічної кривої Безьє.
У програмах векторної графіки існує єдиний спосіб – це інтерактивне переміщення опорних і керуючих точок (рис. 3.2). Якщо переміщуються початкова чи кінцева точки, то крива стане відповідним чином змінюватися (витягуватися чи стискуватися як пружна резинка). Переміщення керуючих точок змінює кривизну відповідної частини кривої Безьє.



а) б) в)
Рис. 2. Способи зміни форми сегмента: а) переміщення сегмента,
б) переміщення опорної точки, в) переміщення керуючої точки
Таким чином, за допомогою переміщення цих чотирьох точок отримують необмежену кількість форм кривих Безьє, яка може бути всього-навсього одним окремим сегментом складного векторного контуру.
У кожному сегменті можна добавляти опорні точки, які теж дозволяють змінювати форму кривої. Добавляння нових опорних точок у межах одного сегмента кривої не протирічить тій умові, що окремі криві з’єднуються в ланцюг. Просто крива Безьє добавляється не до кінця контуру, а розміщується всередині вже існуючого контуру.
Взагалі будь-яка конструкція (векторний контур або векторна форма) створюється з векторних сегментів, кожен із яких ідентичний окремій елементарній кривій Безьє.
Звідси слідує, що між ними утворюються з’єднувальні точки, які деколи називаються вузлами (наприклад, nodes – у графічному редакторі Corel Draw).
Для підтримання співвідношення між елементарними сегментами існують різні типи опорних точок.
3. Типи опорних точок:
1) точки перегину,
2) гладка опорна точка,
3) симетрична опорна точка,
4) тангенціальна опорна точка.
Точки перегину. Цей тип опорної точки, який з’єднує два сегменти, забезпечує незалежність керуючих точок у напрямку і довжині один від одного. Такий стан сегментів називається вигин (рис. 3.3).
Гладка опорна точка. Кутове зчленування сегментів (вигин) далеко не завжди вигідне. Наприклад, для створення кола необхідно забезпечити з’єднання яке в кресленні і в геометрії називають гладкимспряженням, коли одна крива плавно переходить у іншу. Таке зчленування забезпечує гладка опорна точка (smooth) (рис. 3.4).
Симетрична опорна точка. У програмах CorelDRAW передбачений підвид гладкого спряження, який називається симетричний вузол (symm від слова «symmetcal») (рис. 3.5). Сутність його в тому, що керуючі лінії фіксують не тільки по напрямку, але й по величині (довжина направляючих завжди однакова). Якщо одну з них збільшувати чи зменшувати, друга буде синхронно повторювати цю дію.
Тангенціальна опорна точка. У свою чергу, в програмі FreeHand у окремий вид опорних точок виділений випадок гладкого спряженням, прямолінійного і криволінійного сегментів (рис. 3.6). Така точка отримала назву тангенціальної (connecter point). Під час виділення така точка позначається трикутником.
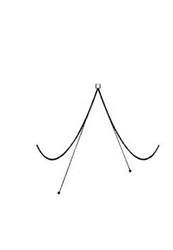

Рис. 3. Приклад точки перегину Рис. 4. Приклад гладкої точки
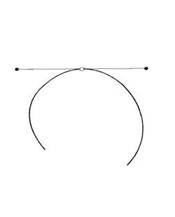

Рис. 5. Симетрична опорна точка Рис. 6. Тангенціальна опорна точка
Зміст цієї точки в тому, що для того, щоб криволінійний сегмент гладко з’єднувався з прямою лінією, дотична криволінійного сегмента повинна співпадати з продовженням прямого сегмента. Тому керуюча точка криволінійного сегмента спроможна рухатися тільки вздовж цієї дотичної. Типи опорних точок у різних векторних програмах подано в табл. 1.
Таблиця 1.
Типи опорних точок у різних векторних програмах
| Тип опорної точки | Adobe Illustrator | Macromedia FreeHand | CorelDRAW |
| Кутова | Corner anchor point | Corner point | Cups node |
| Гладка | Smooth anchor point | Curve point | Smooth node |
| Тангенціальна | - | Connector point | - |
| Симетрична | - | - | Summ node |
Основні редактори векторної графіки
1) Редактор XFig
Цей графічний редактор призначений для роботи в операційній системі Linux і встановлений в графічну оболонку KDE.
Стандартний набір геометричних фігур включає в себе: коло та еліпс із можливостями їх створення по двох різних початкових умовах – радіусу чи діаметру; замкнені і незамкнені лінії, ломані, правильні і неправильні багатокутники, дуги і різні прямокутники.
2) Редактор Adobe Illustrator
Пакет Illustrator свого часу став зразком програм векторної графіки, за своєю потужністю еквівалентний растровому редактору Adobe Photoshop: має аналогічний інтерфейс, дозволяє підключити різні фільтри і ефекти, працює з зображеннями різних форматів, у тому числі .cdr (Corel Draw) і .swf (Flash).
3) Редактор CorelDRAW
Цей редактор на сьогоднішній день є найбільш розповсюдженим редактором векторної графіки. Крім обробки векторної графіки, в пакеті програм канадської фірми Corel існує обробник растрової графіки (Corel PHOTO-PAINT), трасувальник зображень (CorelTRACE), редактор шрифтів, підготовки текстур і створення штрихкодів, а також великі колекції зображень (CorelGallery).
4) Редактор Macromedia FreeHand
Редактор був розроблений фірмою Aldus, потім права на цей редактор перекупила Macromedia. Пакет забезпечує високу зручність роботи з пензликами, ефекти витиснення і трьохмірне обертання векторних об’єктів, може працювати в багатострічковому режимі. Крім цього, FreeHand повністю інтегрований з Flash і іншими продуктами МХ-лінійки Macromedia. Насьогодні редактор перекупила фірма Adobe.
Фрактальна графіка, як і векторна, базується на обчислюванні, й займає проміжне положення між растровою і векторною графікою. Крім того, фрактальні візерунки часто використовують, як фрактальні заливання у редакторах растрової та векторної графіки.
Поняття фракталу було запропоноване математиком Бенуа Мандельбротом в 1975 році для позначення нерегулярних, але самоподібних структур, вивченням яких він займався. Фракталом називається структура, що складається з частин, які в якомусь сенсі подібні до цілого, тобто
фрактал – це складний геометричний об'єкт, який складається з безлічі менших собі подібних об'єктів.
Ще до Бенуа Мандельбротом видатними вченими були відкриті класичні фрактали: множини Кантора, криві Піано, функції Вейєрштрасса, сніжинки Коха, і коврик Серпинського. Але тільки Мандельброт та його учні зуміли звести розрізнені фрактали в єдину струнку науку, відкривши при цьому нові фрактали, які моделювали різні природні об’єкти та явища. Фрактальним підходом можна описувати структури як неживої природи: лінії берегів, рельєф місцевості, обриси хмар, структури корисних копалин, так і живої: системи кровообігу людини, будови нирок і легенів, які нагадують по структурі дерева з кроною, різних процесів: наприклад, турбулентних, які використовуються при прогнозі погоди. Алгоритми фрактальної геометрії використовують для стиснення зображень, в дистанційному зондуванні і радіолокації, моделюванні фракталоподібних природніх систем, еволюційних обчисленнях, тощо.
На рисунку 1.9 показано зображення листа папороті, згенерованого за допомогою фрактальної графіки. В даному випадку яскраво простежується самоподібність.





Рисунок 1.9 – Самоподібність фрактальних фігур (лист папороті)
Роль фракталів в комп’ютерній графіці на цей час є досить великою. За їх допомогою можна задати криві або поверхні дуже складної форми. Фрактальна графіка активно використовується при генерації зображень, яким властива самоподібність – хмар, гір, поверхні моря.
Загалом, в залежності від способу побудови зображення фракталу, всі фрактали поділяються на дві великі групи [19]:
- детерміновані (або класичні) фрактали;
- стохастичні (або випадкові) фрактали.
Детерміновані фрактали розділяють на геометричні та алгебраїчні.
Геометричні фрактали – це найбільш наглядні і найпростіші для розуміння. В двовимірному випадку їх отримують за допомогою деякої ламаної кривої (або поверхні для тривимірного випадку). За кожен крок побудови кожен відрізок ламаної замінюється на „криву-генератор” з відповідною зміною масштабу. В результаті великої кількості повторень цих кроків 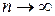 , ми отримаємо геометричний фрактал. На рисунку 1.10 показано побудову геометричного фракталу, відомого під назвою „тріадна крива Коха” для кількості кроків
, ми отримаємо геометричний фрактал. На рисунку 1.10 показано побудову геометричного фракталу, відомого під назвою „тріадна крива Коха” для кількості кроків 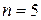 .
.
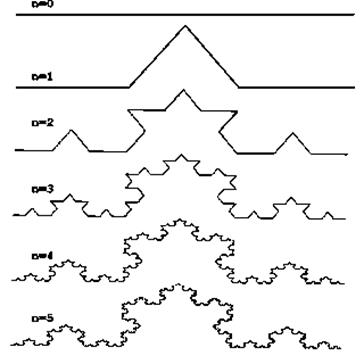
Рисунок 1.10 – Побудова тріадної кривоі Коха
Побудова кривої починається з відрізку одиничної довжини – це нульове покоління кривої Коха. Далі кожен відрізок (в нульовому поколінні одинична лінія) замінюється на „генератор”, який позначений через 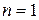 .
.
В результаті такої заміни отримується наступне покоління кривої Коха. В першому поколінні – це крива з чотирьох прямих відрізків, кожний з яких довжиною 1/3. Для генерації наступного покоління виконуються ті самі дії – кожен відрізок замінюється на зменшений утворюючий елемент або „генератор”.
Отже, для отримання кожного наступного покоління, всі відрізки попереднього покоління необхідно замінити зменшеним утворюючим елементом. Крива n-го покоління при будь-якому кінцевому n не є фракталом, а тільки передфрактальним об’єктом. Лише при 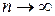 крива Коха стає фрактальним об’єктом.
крива Коха стає фрактальним об’єктом.
Розмірність 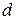 даної кривої визначається як:
даної кривої визначається як:
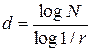 (1.3),
(1.3),
де 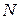 - кількість рівних частин початкового відрізку;
- кількість рівних частин початкового відрізку;
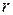 - коефіцієнт подібності.
- коефіцієнт подібності.
В даному випадку 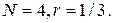 За формулою (1.3) розмірність даного фракталу буде
За формулою (1.3) розмірність даного фракталу буде 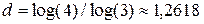 .
.
В результаті отримується крива нескінченної довжини, яка заповнює обмежену множину на площині.
Тріадна крива Коха також використовується для побудови іншого фракталу – сніжинки Коха (рисунок 1.11). Для цього будується рівносторонній трикутник, і описані вище операції проводяться над кожною з його сторін. При  отримується замкнена крива нескінченної довжини, яка охоплює скінченну площу.
отримується замкнена крива нескінченної довжини, яка охоплює скінченну площу.
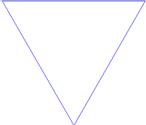


Рисунок 1.11 – Побудова „сніжинки” Коха (0, 1, 2 кроки)
Такий підхід для побудови зображень геометричних фракталів використовується в алгоритмах L-систем (L-systems). Поняття L-систем було розроблено біологом Арістидом Ліндермауером, який використовував їх для побудови зображень, які дуже схожі на природні – листки, траву і т. д. (рисунок 1.12). Метод для побудови зображення отримав назву “turtle-method” або „метод черепашки”.

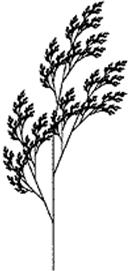
Рисунок 1.12 – Зображення, створені за допомогою L-систем
Для генерації деяких інших геометричних фракталів, наприклад, для трикутника (або ковра) Серпінського використовується інший підхід. Він базується на ітеративному алгоритмі, що полягає в дії на початкову множину стискаючими відображеннями, які на великій кількості ітерацій зводять початкове зображення до зображення фракталу. Цей алгоритм був розроблений американським вченим Майклом Барнслі і отримав назву система ітерованих функцій (СІФ). На рисунку 1.13 зображено фрактал, який називається ковром Серпінського.

Рисунок 1.13 – Трикутник Серпінського
Розмірність даного фракталу за формулою (1.3):
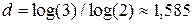 .
.
Алгебраїчні фракталиє найбільшою групою фракталів. Їх отримують за допомогою нелінійних процесів в n-мірних просторах. Найчастіше використовуються двовимірні простори.
Стохастичні фракталиотримуються в тому випадку, коли в ітераційному процесі побудови детермінованого фракталу випадково змінювати які-небудь його параметри. Отримані „рандомізовані” фрактали можуть бути використані для генерування берегової лінії, поверхні моря.
Але для моделювання широкого спектру „природніх” фракталів, таких як гори, хмари, поверхні лісових масивів, простої випадкової зміни одного із параметрів побудови статичного фракталу, не завжди достатньо. Для цієї цілі використовують інший клас фрактальних об’єктів, які базуються на фрактальному броунівському русі – випадковому процесі, який дуже широко представлений в природі (броунівський рух маленьких твердих часток в воді).
За допомогою реалізації броунівського руху на площині, моделюється гірський рельєф (рисунок 1.17).

Рисунок 1.17 – Моделювання гірського рельєфу (броунівський рух на площині)
Зображення фрактального типу використовуються в рекламі, образотворчому мистецтві. Лідером на ринку фрактальної графіки до недавнього часу (тобто до продажу своїх програмних продуктів іншим фірмам) була компанія Meta Creations. Спектр її продуктів охоплює багато областей комп'ютерної графіки. Наприклад,
□ Fractal Design Painter - програма для створення і обробки високохудожніх растрових ілюстрацій;
□ Fractal Design Expression поєднує растрову і векторну техніку компьютерної графіки. Тобто ви малюєте векторні об'єкти як в CorelDRAW або Adobe Illustrator, редагуєте їх по опорних вузлах і виконуєте усі інші векторні операції. Але кожній лінії, фігурі ви можете призначити будь-який растровий тип пензля.
Фрактальна графіка міститься у пакетах для наукової візуалізації для побудови, як найпростіших структур так і складних ілюстрацій, що імітують природні процеси та тривимірні об'єкти.
Серед програмних засобів можна виділити також продукти фірми Golden SoftWare:
· Surfer - створення тривимірних поверхонь;
· Grapher - створення двовимірних графіків;
· Map Viewer - побудова кольорових карт.
Surfer дозволяє обробити та візуалізувати двовимірні набори даних, що описані функцією z=f (x,y). Можна побудувати цифрову модель поверхні, застосувати допоміжні операції і візуалізувати результат.
Grapher призначений для обробки та виводу графіків, що описані функціями y=f(x). Не має обмежень по числу графіків на одному рисунку або числу кривих в одному графіку і дозволяє розмістити декілька осей з різними масштабами та одиницями виміру.
Map Viewer дозволяє вводити та корегувати карти - змінювати масштаб, перетворювати координати, обробляти й виводити у графічному вигляді числову інформацію, пов'язану з картами.
Пакет Iris Explorer (фірма Graphics) призначена для створення моделей погодних умов та океану.
Пакет Earth Watch (фірма Earth Watch) призначений для моделювання та демонстрації тривимірного зображення метеоумов над Землею, будувати топологічні поверхні по космічних знімках і прогнозувати погоду на тиждень вперед.
Модуль Chart у стандартному пакеті MS Office дозволяє легко й наочно створити графіки на основі даних, що знаходяться у таблиці. Користувач може перетворити графіки у любу з 5 основних форм графіків:
· гістограма;
· лінії;
· площі;
· в полярних координатах;
· поверхні.
Також, при зміні даних у таблиці, змінюється відповідне значення у графіку.
Дата добавления: 2016-06-13; просмотров: 4280;
