Дискретні випадкові величини

Означення 1. ВВ X називається дискретною, якщо сукупність її можливих значень є скінченною ( x₁, x₂,..., x_n ) або зліченною (x₁, x₂,..., x_n,...).

Прикладами дискретної ВВ є : 1) кількість деталей, що не задовольняють стандарту, серед обраних для контролю 100 деталей; 2) кількість викликив, що надійдуть на станцію швидкої допомоги за добу; 3) кількість перекручених символів у кодовій комбінації, яка передається по каналу зв’язку з перешкодами ; 4) кількість пострілів до першого влучення в мішень .

Набір ймовірностей 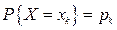(k=1,2,..,n) (або k=1,2,…,n,…) називають розподілом дискретної ВВ X, якасконцентрована в точках x_k . Розподіл містить вичерпну інформацію про випадкову величину.

Дискретну ВВ часто представляють таблицею

X			…
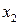
P			…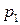

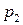
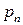
Якщо у проміжок [c; d) попадають лише значення x_i, x_i+1,..., x_j ВВ X, то

.

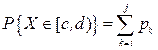(3)

Дійсно, подія XÎ[c; d) є сумою попарно несумісних подій {X= x_i},

{X= x_i+1},…,{X=x_j}. Тому на підставі формули (2) розділу 1.2 про ймовірність суми несумісних подій одержимо:

.

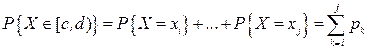Із формули (3) виходять такі наслідки:

1) умова нормування– 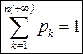(4);

2) Для 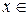(x_k; x_k+1] значення функції розподілу

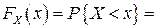
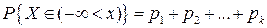, (5)

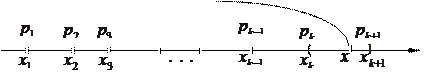
тобто дорівнює сумі ймовірностей подій, для значень 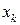ліворуч точки .

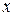Приклад 1. Дискретна ВВ X задається таблицею розподілу.Знайти: 1) С; 2) F_X (x); 3) P{X > – 0.3}

; 4) P{X≤ 1.7}.

Розв’язання. 1) Значення С знаходиться із умови нормування (4) :

0.3+0.1+С+0.35=1 Þ С=0.25. 2) Функцію розподілу знаходимо за наслідком 2 ( рис.2.2).

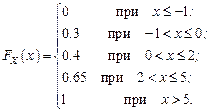3)P{X > – 0.3} = P{X = 0} + P{X = 2}+ P{X = 5}= = 0.7.4)P{X≤ 1.7} = =P{X = 0} + P{X = – 1} = 0.4.

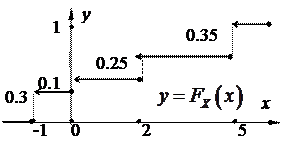Рис. 2.2