Дискретні випадкові вектори

Означення 14.2. Випадковий вектор називається дискретним, якщо його компоненти є дискретними випадковими величинами.

Найбільш повним імовірнісним описанням випадкового вектору є закон розподілу. У випадку системи двох дискретних випадкових величин 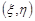закон розподілу найчастіше задається таблицею розподілу (табл. 14.1).

Таблиця 14.1

		…		…
			…		…
			…		…
…	…	…	…	…	…
			…		…
…	…	…	…	…	…

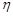
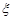
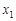
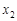
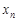
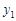
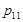
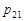
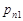
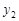
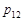
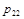
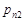
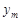
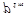
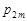
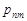
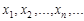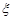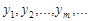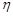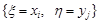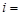У табл. 14.1 – множина значень , – множина значень , . Оскільки події , 1, 2, ...; 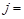1, 2, ... – несумісні та єдино можливі, тобто утворюють повну групу подій, то .

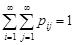За таблицею розподілу системи двох випадкових величин можна знайти закони розподілу окремих компонент. Дійсно, розподіл випадкової величини 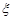отримаємо, якщо обчислимо ймовірність події 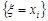(i= 1, 2, …) як суму ймовірностей несумісних подій

. (14.1)

Аналогічно розподіл випадкової величини 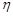отримаємо за формулою

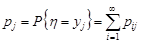. (14.2)

Отже, для того, щоб за таблицею розподілу системи двох випадкових величин (табл. 14.1) знайти закон розподілу компонент, треба додати ймовірності 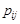з відповідного цьому значенню рядка (або стовпця) даної таблиці.

Приклад 14.1. По каналу зв’язку передають два повідомлення, кожне з яких може незалежно бути спотворено або ні. Імовірність того, що спотворюється перше повідомлення дорівнює 0,2, відповідно ймовірність спотворення другого повідомлення дорівнює 0,1. Введемо випадкові величини 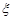та 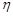, які набувають таких значень: 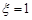, якщо перше повідомлення спотворено; 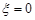, якщо перше повідомлення не спотворено і 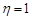, якщо друге повідомлення спотворено; 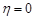, якщо друге повідомлення не спотворено. Скласти таблицю розподілу системи випадкових величин 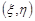та знайти закони розподілу випадкових величин 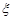та .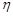

Розв’язання. Для побудови таблиці розподілу системи випадкових величин 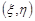треба знайти ймовірності одночасної появи подій 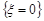, , 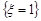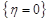та .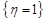

Користуючись теоремою множення ймовірностей для незалежних подій, маємо

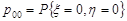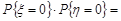= 0,72;

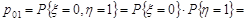0,08;

;

.

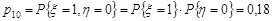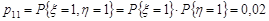Зробимо перевірку результатів:

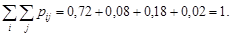
Складемо таблицю розподілу системи 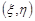(табл. 14.2).

Таблиця 14.2

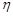
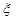
	0,72	0,18
	0,08	0,02

За формулами (14.1) та (14.2) складемо ряди розподілу окремих компонент вектора. Наприклад, для того щоб знайти ймовірності 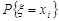, треба скласти ймовірності 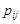, які стоять у таблиці розподілу в стовпці 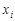(табл. 14.2). Для знаходження ймовірностей 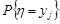додаємо значення 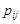, що стоять у таблиці розподілу в рядку 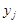. Отже, випадкові компоненти 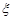та 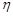мають такі ряди розподілу:

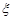
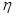
p	0,8	0,2		p	0,9	0,1

Цей результат безпосередньо випливає також і з умови задачі.