Функція розподілу випадкового вектора у випадку n >2

Та її властивості.

Узагальнимо результати попереднього параграфу.

Означення 14.4. Функцією розподілу n-вимірного випадкового вектора 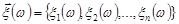називається n дійсних змінних 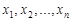вигляду

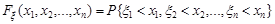. (14.4)

Наведемо властивості функції розподілу (14.4), які є узагальненням відповідних властивостей функції розподілу двовимірної випадкової величини.

1. Функція розподілу будь-якого випадкового вектора є монотонно неспадною функцією по кожному з аргументів, область зміни якої є відрізок .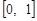

2. 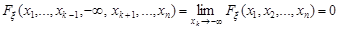, для будь-якого .

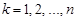3. Якщо один із аргументів функції розподілу (14.4) прямує до 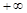, то границя буде функцією розподілу 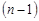-вимірного випадкового вектора :

.

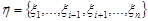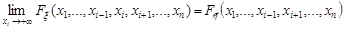Зокрема

,

,

...............................................

.

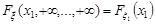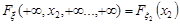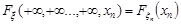Отже, знання функції розподілу випадкового вектора дає можливість отримати функцію розподілу окремих компонент і всіх підсистем системи випадкових величин.

4. .

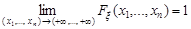5. Функція розподілу випадкового вектора є неперервною зліва функцією по кожному з аргументів.

Приклад 14.3. Довести, що функція

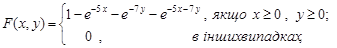
може бути функцією розподілу деякого випадкового вектора .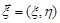

Доведення. Перевіримо виконання властивостей 1 – 5.

1. Очевидно, що .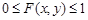

2. .

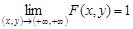3. 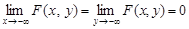(за умовою задачі).

4.

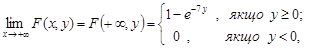
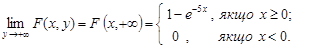
Позначимо .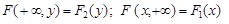

Перевіримо, що ці функції можуть бути функціями розподілу випадкових величин. Неважко перевірити виконання відповідних властивостей тільки для однієї із них, бо вони однотипні, а саме:

1. ;

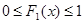2. ;

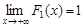3. ;

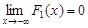4. Функція 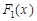є монотонно неспадною функцією.

Отже, функція 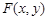може бути функцією розподілу деякого випадкового вектора.