Бета- та гама-функція Ейлера.

СПЕЦІАЛЬНІ ФУНКЦІЇ МАТЕМАТИЧНОЇ ФІЗИКИ.

Практичне застосування диференціальних рівнянь, розв’язок досить різних задач, які відносяться до теплопровідності та динаміці, електромагнітним коливанням та аеромеханіці, квантової механіці та теорії потенціалів приводить до спеціальних функцій.

У наступному розділі міститься кратки але важливі для застосувань властивості основних спеціальних функцій, а також приклади задач, де виникає необхідність їх застосування.

Бета- та гама-функція Ейлера.

За означенням функція Ейлера зображується у вигляді інтегралу

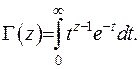(6.1)

Для того, щоби цей інтеграл був збіжний, має виконуватися умова 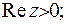відмітимо, що гама-функція може бути комплексною. Встановимо важливу для використання формулу:

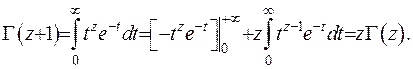
Отже, маємо

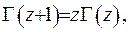(6.2)

або 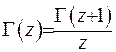. Розглянемо часткові випадки гама-функції. Візьмемо За формулою (6.2) маємо 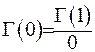, значення 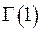за визначенням (6.1) дорівнює 1. Отже, .

При 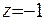за формулою (6.2) здобуваємо 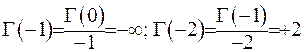і т.д. , тобто у точці 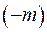гама-функція має полюси першого порядку. Графік гама-функції має вигляд :

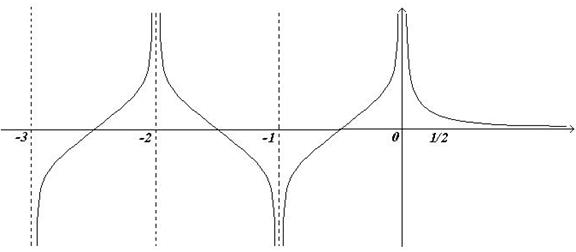
Введемо поняття символу Похгаммера: 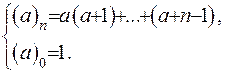За його допомогою зобразимо значення гама-функції для цілих додатних значень аргументу:

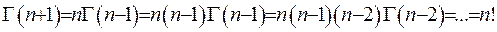(6.3)

Розглянемо інший випадок:

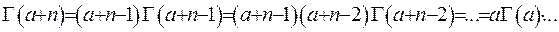
(6.4)

Звідки випливає, що

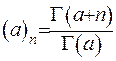(6.5)

Розглянемо випадок, коли 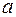є ціле, від’ємне число: .

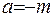1) Нехай :

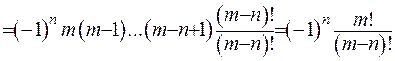
2) Нехай . Спочатку розглянемо окремий випадок .

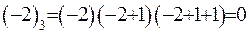, тобто для довільних завжди зустрінеться множник, який буде дорівнювати нулеві. Для від’ємних значень отримано остаточну формулу:

(6.6)

Бета-функція Ейлера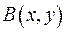

За означенням функція визначається наступним чином

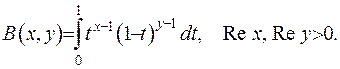(6.7)

Знайдемо зв’язок між бета- та гама-функціями. Для цього зробимо наступну заміну: 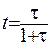. Нижня та верхня межі інтегралу будуть дорівнюватиме:

З урахуванням заміни функція (6.7) набуває вигляду:

(6.8)

Зробимо заміну змінних 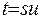у зображенні гама-функції (6.1), тут 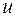- фіксоване число, а - змінна: 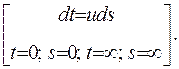З урахуванням заміни зображення (6.1) набуває вигляду:

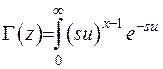
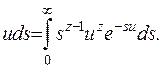(6.9)

Або у іншій формі:

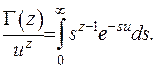(6.10)

У виразі (6.10) покладемо :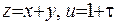

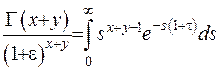. (6.11)

Домножимо обидві частини (6.11) на множник та проінтегруємо на проміжку :

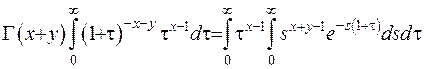. (6.12)

Як бачимо, інтеграл у лівій частині рівності (6.12) за формулою (6.8) є бета-функцією Ейлера. Підрахуємо інтеграл, що стоїть у правій частині:

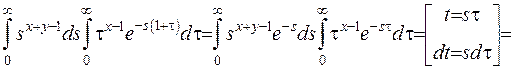
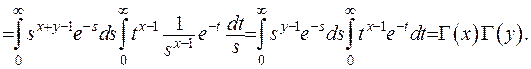
З рівності (6.12) остаточно випливає

(6.13)

та

Як бачимо, бета-функція є симетричною функцією -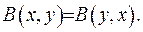

Розглянемо окремі випадки її значень.

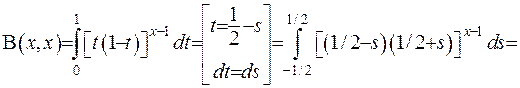
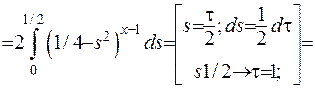
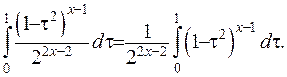
Остаточно отримано:

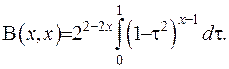(6.14)

Нехай .Тоді (6.15)

З іншого боку, відповідно до формули (6.13):

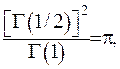де , тобто маємо

. (6.16)

Якщо у формулі (6.14) зробити заміну змінних 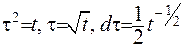, то матимемо:

. (6.17)

Використаємо формулу (6.13) з урахуванням отриманого співвідношення

,

. (6.18)

З формули (6.18) випливає, що :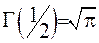

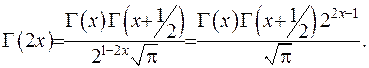(6.19)

Важливою для практики є наступна формула:

(6.20)