Означення та приклади випадкових векторів

В різноманітних випадкових явищах часто розглядають не одну випадкову величину, а систему випадкових величин. Наведемо декілька прикладів.

1. Успішність студента, який закінчив навчання в університеті, характеризується системою n випадкових величин 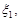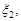..., 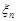– оцінками, які стоять у дипломі.

2. Стан обчислювальної машини в деякий момент часу характеризується системою багатьох випадкових величин: кількість елементів оперативної пам’яті, які зайняті обробкою інформації; час, що пройшов з моменту останньої відмови ЕОМ; кількість елементів, які відмовили і таке інше.

3. Погода в даній місцевості може бути охарактеризована такою системою випадкових величин: 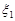– температура, 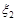– тиск, 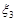– вологість, 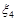– швидкість вітру тощо.

Конкретний набір випадкових величин, які вводять у вивчення, залежить від того, яка задача розв’язується.

Дамо теоретико-множинне трактування випадкового вектора або системи випадкових величин.

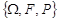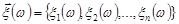
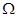Означення 14.1. Нехай – ймовірнісний простір стохастичного експерименту. Назвемо n-вимірним випадковим вектором або системою випадкових величин векторну функцію, яка визначена на просторі та має значення у n-вимірному евклідовому просторі 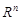. Крім того, поді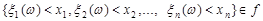я , для 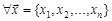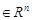. Випадкові величини 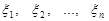називаються координатами або компонентами випадкового вектора.

В подальшому основні поняття будемо розглядати на прикладі двовимірних випадкових векторів або системи з двох випадкових величин 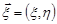. Геометрично двовимірний випадковий вектор можна зобразити точкою на площині, яка має випадкові координати. Таку точку будемо називати випадковою точкою. Аналогічно випадкова точка в трьохвимірному просторі є геометричною інтерпретацією системи трьох випадкових величин.