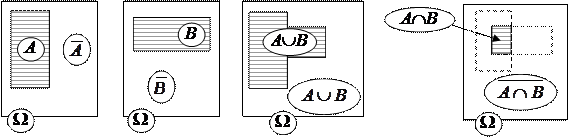Алгебра випадкових подій

Множина, на якій означені операції суми та добутку подій, в математиці називається алгеброю.У просторі W означимо поняття суми та добуткуподій. Алгебра подій дає математичний опис можливих наслідків випробування.

Означення 1.Подія, яка полягає в тому, що наступає принаймні одна з подій А або B, називається об¢єднанням або сумоюцих подій(рис.1.3,а, б,в). Таку подію будемо позначати АÈB або A+B .

а б в Рис. 1.3. г

Означення 2.Подія, яка полягає в тому, що наступають обидві події А та B, називається перерізом або добутком цих подій (рис.1.3, а,б,г). Таку подію будемо позначати А Ç B або A·B.

Із означення операцій È та Ç випливають такі співвідношення:

А + А=А, А А=А, А + W=W, А W=А, А (B + С)=(А B) +(А С).

Операції + та пов‘язані одна з одною двома важливими формулами:

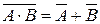а) , б) . (1)

Означення 3. Події АтаB називаються несумісними, якщо їх переріз є неможливою подією:

A 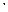B=Æ . (2)

Зрозуміло, якщо події АтаB є несумісними, то будуть несумісними також події А·C іB·C.

Означення 4.Попарно несумісні події А_i (i=1,2,...,n) утворюють повну систему подій (розбиття W), якщо їх сума є вірогідною подією:

А₁+А₂+...+А_n= W, А_i·А_k = Æ (i¹k).

Події А та` 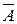утворюють повну систему подій :

А + 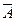= W , А =Æ .

Приклад 3.Проводяться два постріли по мішені. Позначимо через А_i (i=1,2) подію, що полягає у попаданні по мішені при i-тому пострілі. Потрібно виразити через А_i події А таB, які відповідно означають, що в мішені буде: а) точно одна А пробоїна; б) хоча б одна пробоїна.

Розв’язання. а) А = 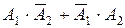(доданки суми є несумісними подіями); б) В =А₁+А₂(доданки суми є сумісними подіями) або В = 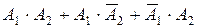(доданки суми є несумісними подіями, але не утворюють повної системи подій).