Первісні поняття. Подія

ЛЕКЦІЇ З ТЕОРІЇ ЙМОВІРНОСТЕЙ ДЛЯ ФЕТ

Теорія ймовірностей вивчає математичну модель реального випробування , наслідок якого неможливо заздалегідь передбачити. При цьому припускається, що таке випробування може бути повторено необмежену кількість разів при незмінних основних умовах. Комплекс другорядних умов, які неможливо проконтролювати, змінюється від випробування до випробування. Саме ці умови приводять до того, що результати однотипних випробувань можуть бути різними.

Позначимо через W множину всіх можливих взаємно виключних наслідків випробування ( припускаємо, що ця множина є відомою до здійснення випробування ). Множина W та її різні підмножини використовуються при побудові імовірнісної моделі цього випробування. МножинуW називають простором елементарних подій. При цьому, кожному наслідку випробування ставиться у відповідність одна і тільки одна точка простору W – елементарна подія w.

Означення 1. Випадкова подія(далі просто подія) – будь-який факт, який може наставати чи не наставати в результаті проведення випробування, причому заздалегідь невідомо, чи з’явиться він чи ні ( тобто, подія є непередбаченим результатом випробування). Для кожної випадкової події A і кожної елементарної події 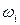можна сказати, сприяє чи ні елементарна подія 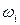появі події A.

Означення 2. Подію A можна розглядати як підмножину W, яка складається з тих точок 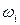, що сприяють появі події A.

Рисунок 1.1 відповідає тому випадку, коли елементарна подія w₁ сприяє події A, а елементарна подія w₂

не сприяє. Множина W може бути як дискретною (рис.1.2,а), так і неперервною (рис.1.2,б,в). У першому випадку вона складається із скінчен-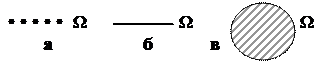

Рис.1.2

ної або зчисленної (такої, яку можна перерахувати) кількості точок, а у другому – із незчисленної кількості точок.

Приклад 1. Підкидається гральний кубик (кубик, зроблений з однорідного матеріалу, грані якого позначені числами 1,2,3,4,5,6). Результатом випробування (спостереження) є число, що випало на верхній грані кубика.

Простір W складається з шести точок w_i, де через w_i позначено елементарні події, що відповідають випаданню грані, на якій написано число i (i=1,2,3,4,5,6): W{w₁,w₂,w₃,w₄,w₅,w₆}. Події A (випадання парного числа) сприяють елементарні події w₂, w₄, w₆ – A{w₂,w₄,w₆}.

Приклад 2. Монета підкидається тричі..Елементарні події мають вигляд 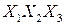, де – Г або Ц. Простір W{ГГГ, ГГЦ, ГЦГ, ЦГГ, ГЦЦ, ЦГЦ, ЦЦГ, ЦЦЦ}, Подія В випадання не менщ двох гербів В{ГГГ, ГГЦ, ГЦГ, ЦГГ}.

Означення 3-4. Подія, що наступає при будь-якому наслідку випробування, називається вірогідною. Вона співпадає з множиною W і позначається надалі також літерою W. Подія, яка не наступає ні при жодному з наслідків випробування називається неможливою. Вона співпадає з пустою множиною і надалі позначається символом Æ. В умовах прикладу 1 випадання не більше шести очок – вірогідна подія, а випадання семи очок – неможлива.

Відзначимо, що коли дискретний простір W якогось випробування складається з n точок, то кількість всіх подій, пов’язаних з цим випробуванням дорівнює 2ⁿ. Інакше кажучи, множина усіх підмножин множини, яка містить n елементів, складається з 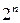елементів

Означення 5. Подія 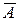, яка полягає в тому, що подія А не наступає, називається протилежною події А або запереченням А ( 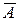доповнює множину А до W: 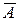=W\А). Зрозуміло, що 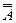= А, =Æ .В умовах прикладу 1 подія 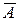{w₁,w₃,w₅}.