Операції над подіями
Оскільки випадкові події – це підмножини простору елементарних подій  , то операції над множинами можна перенести на операції над подіями.
, то операції над множинами можна перенести на операції над подіями.
Включення АÌВ означає, що подія В відбулася, якщо відбулася подія А. Тобто з появи події А випливає поява події В. Очевидно 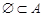 ,
,  .
.
Приклад 1.7. Із колоди у 52 гральні карти навмання виймають одну карту. Розглянемо дві випадкові події: 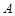 ={витягнута карта – пікової масті},
={витягнута карта – пікової масті},  = {витягнута карта – чорної масті}. Очевидно, що
= {витягнута карта – чорної масті}. Очевидно, що  .
.
Об’єднанняподій А 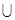 В – це подія, яка відбувається, якщо відбувається хоча б одна з подій А або В. Об’єднувати можна і нескінченну кількість подій. Результат цієї операції позначають через
В – це подія, яка відбувається, якщо відбувається хоча б одна з подій А або В. Об’єднувати можна і нескінченну кількість подій. Результат цієї операції позначають через 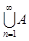 n.
n.
Приклад 1.8. Гральний кубик підкидається один раз. Випадкова подія 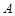 полягає в тому, що випаде 2 очка, випадкова подія
полягає в тому, що випаде 2 очка, випадкова подія  полягає в тому, що випаде парна кількість очок. Об’єднання А
полягає в тому, що випаде парна кількість очок. Об’єднання А 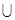 В – це випадкова подія, яка полягає в тому, що випаде парне число очок.
В – це випадкова подія, яка полягає в тому, що випаде парне число очок.
Мають місце такі властивості операції об’єднання випадкових величин:
1. 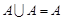 ; 2.
; 2.  ;
;
3. якщо  , то
, то  ; 4.
; 4.  ;
;
5.  ; 6.
; 6. 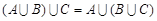 .
.
Перетин подій А 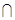 В – це подія, яка відбувається, якщо відбувається і подія А, і подія В. Перетинати можна і нескінченну кількість подій. Результат цієї операції позначають через
В – це подія, яка відбувається, якщо відбувається і подія А, і подія В. Перетинати можна і нескінченну кількість подій. Результат цієї операції позначають через  n.
n.
Приклад 1.9. Гральний кубик підкидається два рази. Розглянемо три випадкові події, пов’язані із значенням суми двох очок, що випали при двох підкиданнях: 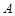 ={сума очок не перевищує 5};
={сума очок не перевищує 5};  ={сума очок більше 7};
={сума очок більше 7};  ={сума очок менша 8}. Очевидно, що
={сума очок менша 8}. Очевидно, що
 .
.
Мають місце такі властивості операції перетину випадкових величин:
1.  ; 2.
; 2. 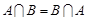 ;
;
3.  ;
;
4. якщо  , то
, то  ;
;
5. 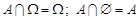 ;
;
6. 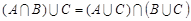 ;
;
7.  ,
, 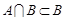 ;
;
8. 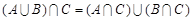 .
.
Означення 1.7. Випадкові події 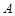 та
та  називаються несумісні, якщо вони не можуть відбуватися одночасно, тобто
називаються несумісні, якщо вони не можуть відбуватися одночасно, тобто 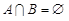 .
.
Події А1, А2, ..., Аn утворюють повну групу подій:
а) якщо  i = W; б) якщо Аi
i = W; б) якщо Аi 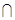 Аj=Æ, i¹j; такі події називаються попарно несумісними.
Аj=Æ, i¹j; такі події називаються попарно несумісними.
Приклад 1.10. Виконується два постріли в мішень. Розглянемо події А ={одне влучення в мішень}, B ={два влучення в мішень}, С ={жодного влучення в мішень}. Ці події утворюють повну групу подій.
Кожній події А можна поставити у відповідність протилежнуподію 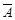 , яка відбувається тоді, коли А не відбувається. Очевидно,
, яка відбувається тоді, коли А не відбувається. Очевидно, 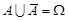 та
та 
Приклад 1.11. Папірці із літерами розрізаної абетки навмання розкладають один за одним. Випадкова подія полягає в тому, що принаймні одна літера влучить на те місце, яке відповідає її розташуванню у абетці. Тоді протилежна їй подія полягає в тому, що жодна літера не буде на своєму місці за абеткою.
В багатьох задачах теорії ймовірностей зустрічається термін “таблиця випадкових чисел”. Ці таблиці можна будувати різними методами. Запропонуємо один із них. Нехай на папірці нескінченної довжини записано число 0 та всі числа натурального ряду. Розріжемо цей папірець на окремі таким чином, щоб на кожному із них залишилась записаною лише одна цифра. Потім всі папірці перемішують і навмання витягають один. Цифру, що записана на цьому папірці, заносять у таблицю, а папірець повертають до всіх інших. Цю процедуру повторяють нескінчену кількість разів. Так отримують таблицю випадкових чисел. Аналогічно можна будувати таблицю двозначних випадкових чисел, вибираючи кожен раз навмання два числа і т. д.
Приклад 1.12. Із таблиці випадкових чисел навмання відбирається число. Випадкова подія полягає в тому, що це число закінчується на цифру 5 або 0. Протилежна подія полягає в тому, що це число не ділиться на 5.
РізницяА\В подій – це подія, що відбувається тоді, коли відбувається подія А і не відбувається подія В. Очевидно, що 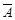 = =W\A, А\В =
= =W\A, А\В = 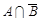 .
.
Мають місце правила де Моргана:
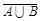 =
=  ,
,  .
.
Дата добавления: 2016-11-02; просмотров: 1026;
