Теорії ймовірностей
Теоретико-множинний підхід в теорії ймовірностей полягає в тому, що кожному стохастичному експерименту ставиться у відповідність простір елементарних подій W, елементами якого є елементарні події w.
Означення 1.6. Елементарні події – це логічно єдино можливі результати експерименту, які взаємно виключають один одного.
Приклад 1.4. Стохастичний експеримент полягає в киданні один раз грального кубика. Простір елементарних подій, який описує цей експеримент, складається з шістьох елементарних подій 
{випала грань з k очками}, k=1, 2, …, 6.
Приклад 1.5. Стохастичний експеримент полягає в киданні монети до першої появи герба. Простір елементарних подій, який описує цей експеримент, складається з нескінченної кількості елементарних подій {герб випав при k киданні монети}, k=1, 2, … .
Приклад 1.6. Стохастичний експеримент полягає в тому, що радіоприймач у деякому інтервалі часу Т приймає деякий сигнал 
. Простір елементарних подій можна трактувати як множину функцій , які задані на проміжку Т.
Отже, з наведених прикладів випливає, що простір елементарних подій може мати скінчену, злічену або незлічену кількість елементарних подій.
Кожна випадкова подія А інтерпретується як підмножина простору елементарних подій W. Подія А відбулася, якщо відбулася будь-яка подія wÎА. Неможливу подію доречно трактувати як порожню множину, тому надалі вона позначається символом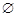 
. Вірогідна подія повинна містити всі елементарні події, оскільки вона відбувається завжди. Звідси вірогідну подію інтерпретують як весь простір елементарних подій і позначають відповідно літерою W.
Дата добавления: 2016-11-02; просмотров: 401;