Початкові поняття теорії ймовірностей

Введемо початкові поняття теорії ймовірностей.

Означення 1.1. Стохастичним експериментом (випробуванням, дослідом) називається будь-який експеримент який можна неодноразово повторювати за деяких незмінних умов і результат якого передбачити заздалегідь не можна.

Означення 1.2. Подія – це будь-який результат стохастичного експерименту.

Події бувають: випадкові, неможливі, вірогідні.

Означення 1.3. Назвемо подію випадковою, якщо в даному стохастичному експерименті вона може відбутися чи не відбутися.

Домовимось в подальшому випадкові події позначати великими літерами латинської абетки.

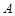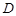Приклад 1.1. Дехто по виході із своєї квартири зустрічає першу на своєму шляху людину. Це є стохастичний експеримент. Випадковими подіями цього стохастичного експерименту можуть бути: = {ця людина – чоловік}; = {ця людина – жінка}; ={ця людина – дитина}; = {ця людина – дівчинка}. Зауважимо, що для коректності визначення подій 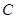та 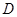треба домовитись до якого віку людину вважати дитиною.

Приклад 1.2. Дехто по виході із свого будинку зустрічає першу на своєму шляху автомашину і записує її номер. Всі номери чотиризначні, окрім номера 0000. Це є стохастичний експеримент. Випадковими подіями в цьому стохастичному експерименті будуть події: 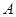={номер не має цифри 5}; 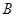={номер – парне число};

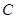= {номер ділиться на 3}; 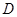={номер не має однакових цифр}.

Означення 1.4. Назвемо подію вірогідною, якщо вона завжди відбувається в стохастичному експерименті.

Означення 1.5. Назвемо подію неможливою, якщо вона ніколи не відбувається в стохастичному експерименті.

Приклад 1.3. Стохастичний експеримент полягає в киданні один раз грального кубика (кубик із шістьма гранями, на кожній з яких стоять цифри від 1 до 6 ). Прикладом неможливої події може бути подія, яка полягає в тому, що випало 10 очок; вірогідної – випало не більше 6 очок; випадкової – випало 2 очка.