Неперервні випадкові величини, щільність розподілу ймовірностей неперервної випадкової величини та її властивості

Означення 10.1. Нехай 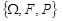– імовірнісний простір, на якому задана випадкова величина 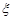. Назвемо її неперервною, якщо функція розподілу 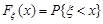є неперервною, диференційовною майже скрізь, за винятком можливо окремих ізольованих точок.

Тоді, як було показано в лекції 9, для такої величини 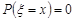. Отже, є сенс казати про щільність розподілу ймовірностей в точці x. Введемо це поняття.

Означення 10.2. Щільність розподілу ймовірностей неперервної випадкової величини 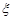дорівнює границі (якщо вона існує)

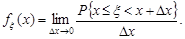(10.1)

Закон розподілу неперервної випадкової величини 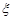найчастіше задається щільністю розподілу ймовірностей.

Розглянемо властивості щільності розподілу ймовірностей.

1. Зв’язок між щільністю розподілу неперервної випадкової величини 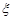та функцією розподілу такий:

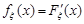Доведення. Із означення 10.2 маємо

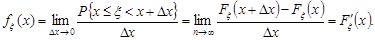
2. Щільність розподілу ймовірностей 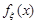є невід’ємною функцією.

Це випливає з того факту, що похідна монотонно неспадної функції, якою є функція розподілу випадкової величини, – невід’ємна.

3. Функція розподілу неперервної випадкової величини 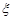визначається за щільністю розподілу так:

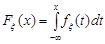. (10.2)

Доведення. Із означення 10.2 випливає, що функція розподілу неперервної випадкової величини 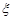є первісна щільності розподілу ймовірностей. Отже, за формулою Ньютона-Лейбніца

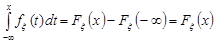4. Щільність розподілу ймовірностей 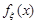задовольняє умові нормування:

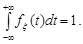
Доведення. Із властивості 3 щільності розподілу ймовірностей 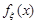та властивості 2 функції розподілу 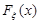маємо

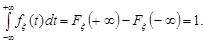
5. Імовірність попадання випадкової величини 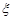в будь-який проміжок 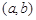можна обчислити за формулою

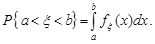(10.3)

Доведення. Із властивості 3 щільності розподілу ймовірностей 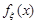та властивості 5 функції розподілу 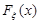маємо

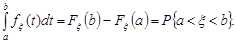
Зауваження. В якості проміжку можна розглядати відрізок чи півінтервал. Це випливає з того, що для неперервної випадкової величини 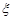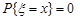для 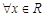, а тому,

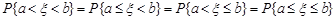Означення 10.3. Графік щільності розподілу ймовірностей неперервної випадкової величини 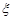називається кривою розподілу.

Властивості щільності розподілу ймовірностей 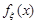допускають таку геометричну інтерпретацію.

1. Крива розподілу ймовірностей неперервної випадкової величини 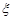повністю розташована в верхній півплощині .

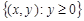2. Імовірність попадання випадкової величини 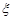в будь-який проміжок 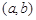чисельно дорівнює площі криволінійної трапеції, яка обмежена відповідною частиною кривої розподілу, прямими 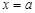, 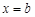та відрізком 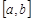осі абсцис.

3. Вся площа, яка обмежена кривою розподілу та віссю абсцис, дорівнює 1.

4. На рис. 10.1 наведена крива розподілу деякої неперервної випадкової величини 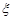. Аналітичний запис щільності розподілу ймовірностей цієї випадкової величини є

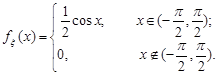
Тоді значення функції розподілу 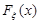в точці 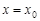дорівнює площі області, яка заштрихована.

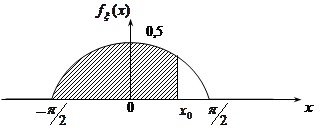Рис. 10.1

Щільність розподілу ймовірностей іноді називають диференціальним законом розподілу неперервної випадкової величини. При вивченні конкретних фізичних явищ, які характеризуються випадковою величиною, останні мають відповідну розмірність. За означенням функція розподілу випадкової величини 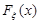є безрозмірною характеристикою, а щільність розподілу ймовірностей 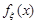має розмірність, яка обернена розмірності випадкової величини 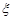. Так, наприклад, якщо випадкова величина 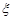вимірюється в метрах, то її щільність розподілу 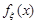буде вимірюватись в одиниці на метр.

Приклад 10.1. Неперервна випадкова величина 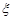має щільність розподілу ймовірностей, графік якої зображено на рис. 10.2 (закон Сімпсона).

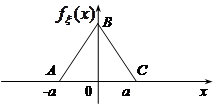Рис. 10.2

Записати аналітичні вирази функцій 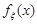та 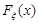. Знайти ймовірність події .

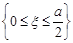Розв’язання. 1. Для того, щоб записати аналітичний вираз 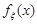треба знайти ординату точки В. З умови нормування випливає, що площа трикутника АВС дорівнює 1. Отже, 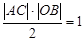. Звідси 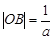. За формулою рівняння прямої, яка задана двома точками, маємо

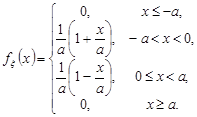
Запис цієї формули може бути коротшим

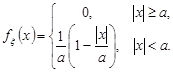
2. Функцію розподілу 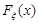знайдемо за формулою (10.2).

Тоді:

а) якщ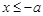о , то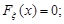

б) якщ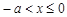о , то

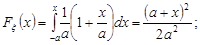
в) якщ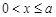о , то

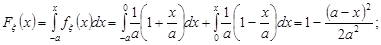
г) якщ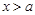о , то

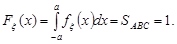
Усі знайдені вирази зведемо в одну формулу:

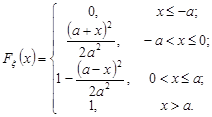
3. Імовірність події 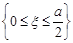обчислимо за формулою (10.3).

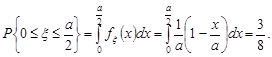
На закінчення зауважимо, що крім дискретних та неперервних випадкових величин існують випадкові величини мішаного типу. Випадкова величина називається мішаною,якщо її функція розподілу на деяких проміжках монотонно зростає і має розриви першого роду в окремих точках. Крім того, можна побудувати випадкову величину, яка не буде ні дискретною, ні неперервною, так звану сингулярну випадкову величину. Але найбільш практичне значення мають дискретні та неперервні випадкові величини. Саме такі величини будуть вивчатися далі.

<== предыдущая лекция	\|	следующая лекция ==>
Операції над подіями	\|	МЕЖДУНАРОДНЫЙ КРЕДИТ КАК ЭКОНОМИЧЕСКАЯ КАТЕГОРИЯ

Дата добавления: 2016-11-02; просмотров: 2225;