Принцип практичної вірогідності
Застосування результатів теорії ймовірності грунтується на “принципі практичної вірогідності”. А саме, якщо ймовірність настання події A достатньо близька до 1, то при одноразовому проведенні випробування слід знехтувати можливістю настання малоймовірної події`A. У цих умовах A та`A називають відповідно практично вірогідною та практично неможливою подіями.
Визначення тієї межі, починаючи з якої подію слід вважати практично неможливою, знаходиться за рамками теорії ймовірностей. Ясно, що чим більші збитки може принести нехтування можливості настання події, тим меншою повинна бути межа. Одна і таж ймовірність може бути малою в однієї ситуації і неприпустимо великою в іншій. Наприклад, межа 0.01 достатня для того, щоб вважати практично неможливим перегорання нової електричної лампочки, але абсолютно недопустима для того, щоб вважати практично неможливою аварію скафандра космонавта або парашута .
Теорема множення та її наслідки
Умовна ймовірність
Нехай АтаB є подіями, пов’язаними з деяким випробуванням і P(B)>0.
Означення 1. Умовною ймовірністю P(АïB) події А за умови здійснення події B називається відношення
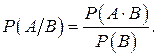
| (1) |
Умовна ймовірність задовольняє аксіомам імовірності 1-3 пункту1.2.2 :
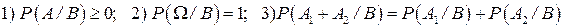 ,
,
якщо 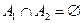 .
.
Із співвідношення (1) негайно випливає теорема множення ймовірностей
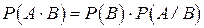 . .
| (2) |
Якщо поміняти А і В місцями, то теорема множення може бути записана у вигляді
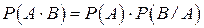 . .
| ( 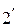 ) )
|
Теорема множення дозволяє знайти ймовірність добутку подій, якщо із змісту задачі зрозумілі (або обчислюються) значення умовних ймовірностей. Вона узагальнюється на випадок скінченного числа множників. Наприклад,

Приклад 1. Ймовірність аварії при запуску ракети дорівнює 0,15. Ймовірність аварії на старті є 0,12. Яка ймовірність аварії при умові успішного старту.
Розв’язання. Нехай подія A полягає у тому, що запуск ракети успішний, а подія B - це успішний старт ракети. Із умов задачі випливає, що A·B=A. Отже,

Таким чином, P( 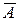 /B)=1–P(A/B)=0.034.
/B)=1–P(A/B)=0.034.
Означення 2. Подія А називається незалежною від події B, якщо
P(АïB)=P(А) (P(B)>0).
Нехай подія А незалежна від події B і P(A)>0. Тоді з формул (2) та (2¢) випливає, що подія B незалежна від події А. Таким чином, поняття незалежності подій є взаємним.
Події А та B незалежні тоді і тільки тоді, коли виконується рівність
 . .
| (3) |
Якщо події А та B незалежні, то будуть незалежними такі пари подій: `А та B, А та`B,`А та`B (наприклад, незалежність подій А та`B можна довести таким чином 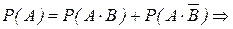
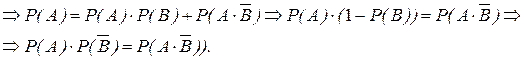
Якщо події A i B (P(A)>0,P(B)>0) несумісні, то вони є залежними :
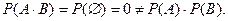
Відзначимо, що коли Р(А)=0 ,то події А і В є незалежними :
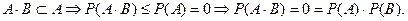
У тому випадку, коли кількість подій перевищує два, вводиться поняття незалежних у сукупності(взаємно незалежних) подій. Останнє означає, що ймовірність якої-небудь події не залежить від здійснення інших. Наприклад, для трьох подій А1, А2, А3, незалежних у сукупності, повинні виконуватись співвідношення P(A1/A2)=P(A1), P(A1/A3)=P(A1), P(A1/A2·A3)=P(A1), P(A2/A3)=P(A2), P(A2/A1·A3)=P(A2), P(A3/A1·A2)=P(A3). Для подій А1, А2,..., Аn, незалежних у сукупності, справедливе співвідношення
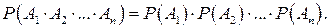
| (3¢) |
Приклад 2. Проводиться два постріли по мішені. Ймовірності влучення при першому та другому пострілі дорівнюють відповідно 0.3 і 0.6. Яка ймовірність, що у мішені буде: а) точно одна пробоїна; б) хоча б одна пробоїна?
Розв’язання. Позначимо через Ai (i=1,2) подію, яка полягає у тому, що при i–му пострілі буде попадання у мішень. Події A1 та A2 незалежні, але сумісні.
а) Нехай A – подія , яка полягає у тому, що у мішені буде точно одна пробоїна. Тоді 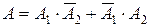 . Оскільки події
. Оскільки події 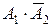 і
і 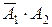 несумісні, то на підставі аксіоми 3 і теореми множення ймовірностей одержимо
несумісні, то на підставі аксіоми 3 і теореми множення ймовірностей одержимо
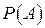 =
= 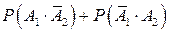 =
= 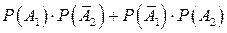 =0.3
=0.3  0.4+0.7
0.4+0.7  0.6=
0.6=
=0.54.
б) Нехай B – подія , яка полягає у тому, що в мішені буде хоча б одна пробоїна. Тоді B=A1+A2 і на підставі теорем додавання та множення ймовірностей матимемо
 =
= 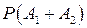 =
= 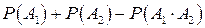 =
= 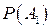 +
+ 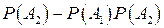 =
=
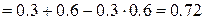 .
.
Інший спосіб розв’язку: 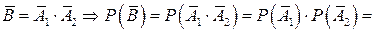
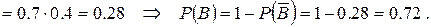
Дата добавления: 2016-10-17; просмотров: 787;
