Приклад 2. В умовах прикладу 1 навмання обраний ігрок забив пенальті. Знайти ймрвірність того,що це був нападник, півзахисник, зажисник, вратар.
Розв’язання. За формулою (5) 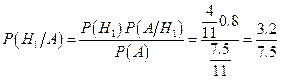 . Так само одержимо
. Так само одержимо
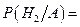
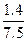 ,
, 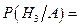
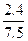 ,
, 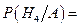
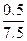
Приклад 3. Надійність приладів (ймовірність безвідмовної роботи протягом заданого проміжку часу) в залежності від якості одного з елементів дорівнює відповідно 0.95, 0.9, 0.8. Відомо, що 20% приладів випускають у першому варіанті, 30% – у другому і 50% – у третьому. Довільно вибраний прилад безвідмовно працював протягом заданого проміжку часу. Яка ймовірність, що він був виконаний в кожному з варіантів?
Розв’язання. Позначимо через A подію, яка полягає у безвідмовній роботі приладу. Нехай гіпотеза Hk (k=1,2,3) означає, що прилад виконано у k-му варіанті. Тоді апріорні ймовірності гіпотез та умовні ймовірності A дорівнюють:
P(H1)=0.2, P(H2)=0.3, P(H3)=0.5,
P(A/H1)=0.95, P(A/H2)=0.9, P(A/H3)=0.8.
За формулами Бейєса знаходимо апостеріорні ймовірності гіпотез
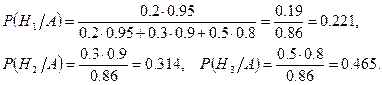
Приклад 4. Двоє стрільців роблять по одному пострілу. Ймовірність попадання по мішені для першого стрільця – 0.7, а для другого – 0.8. У мішені знайдено одну пробоїну. Яка ймовірність того, що у мішень попав перший стрілець?
Розв’язання. Подія A означає наявність однієї пробоїни в мішені. Введемо гіпотези H1 – обидва стрільці не попадають, H2 – перший стрілець попадає, другий ні, H3 – другий стрілець попадає, перший ні, H4 – обидва стрільці попадають. Знайдемо апріорні ймовірності гіпотез:
P(H1)=0.3·0.2=0.06, P(H2)=0.7·0.2=0.14,
P(H3)=0.3·0.8=0.24, P(H4)=0.7·0.8=0.56.
Умовні ймовірності події A дорівнюють:
P(A/H1)=0, P(A/H2)=P(A/H2)=1, P(A/H4)=0.
Таким чином, апостеріорна ймовірність гіпотези H2 така
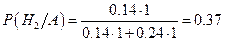 .
.
Дата добавления: 2016-10-17; просмотров: 745;
