Розділ 2. Випадкові величини

Означення 1. Випадковою величиною називається змінна величина, набуваємі значення якої залежать від наслідку експерименту (заздалегідь, до проведення експерименту, визначити, яке значення прийме величина неможливо ). Інакше кажучи, випадковою величиною називається числова функція, яка визначена на просторі елементарних подій W.

Для позначення випадкової величини найчастіше використовуються великі літери X, Y, Z латинського алфавіту, а для їх можливих значень – відповідні малі літери x, y, z.

Наведемо кілька прикладів випадкових величин: 1) кількість влучень у ціль при п‘яти пострілах; 2) кількість відмов приладу протягом заданого проміжку часу; 3) тривалість проміжку часу очікування трамвая або автобуса на зупинці; 4) результат вимірювання фізичної величини; 5) відстань від точки влучення в мішень до її центра .

Випадкова величина дає змогу разом з простором W розглянути інший більш простий простір W₁, у якому елементарні події є значеннями випадкової величини.

Означення 2. Функцією розподілу випадкової величини X називається задана на всій осі Ox функція , яка визначається співвідношенням

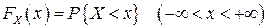	.	(1)
Рис. 2.1

Відзначимо таки властивості функції розподілу:

1) 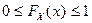( ймовірність довільної події належить відрізку [0;1] );

2) 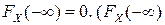= 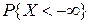, а подія {X< 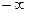} є неможливою ) ;

3) 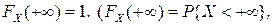а подія { X<+ 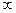}є вірогідною );

4) F_X (x) є неспадною функцією змінної х (якщо с<d , то подія {X<d} є сумою несумісних подій {X<c} і { 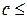X<d} (рис. 2.1)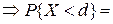

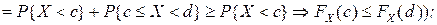
5) функція F_X (х ) в довільній точці є неперервною зліва.

Знаючи функцію розподілу, можна знайти ймовірність того, що випадкова величина попадає у проміжок [c; d) (рис.2.1.)

.