Дискретні випадкові величини
Означення 9.2. Випадкова величина 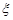 називається дискретною, якщо вона набуває скінчену або зчисленну множину значень.
називається дискретною, якщо вона набуває скінчену або зчисленну множину значень.
Можливі значення дискретної випадкової величини записують у вигляді числової послідовності 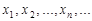 . Випадкова величина вважається заданою, якщо відомі всі її можливі значення та ймовірності, з якими ці значення набуваються.
. Випадкова величина вважається заданою, якщо відомі всі її можливі значення та ймовірності, з якими ці значення набуваються.
Означення 9.3. Законом розподілу будь-якої дискретної випадкової величини 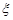 називається співвідношення, яке визначає залежність між значеннями випадкової величини та ймовірностями, з якими ці значення набуваються.
називається співвідношення, яке визначає залежність між значеннями випадкової величини та ймовірностями, з якими ці значення набуваються.
Закон розподілу дискретної випадкової величини 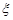 найчастіше задається рядом розподілу (табл. 9.1).
найчастіше задається рядом розподілу (табл. 9.1).
Таблиця 9.1
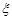 ( ( 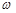 ) )
| 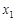
| 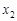
| . . . | 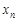
| . . . |
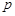
| 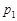
| 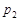
| . . . | 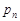
| . . . |
У табл. 9.1: 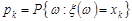 , k = 1, 2,..., n,... .
, k = 1, 2,..., n,... . 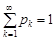 .
.
Наведемо приклад складання закону розподілу дискретної випадкової величини.
Приклад 9.1. Перевіряють деталі в режимі перевантаження. Імовірність пройти випробування для кожної деталі дорівнює 0,8. Випробування незалежні одне від одного і закінчуються одразу, як тільки деталь, яку перевіряють, виходить з ладу. Скласти ряд розподілу випадкової величини 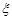 , яка задає кількість випробувань.
, яка задає кількість випробувань.
Розв’язання. Дискретна випадкова величина 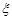 може набувати нескінченної кількості значень: x1=1,
може набувати нескінченної кількості значень: x1=1, 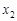 =2, ...,
=2, ..., 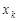 = k, ... Для знаходження ймовірностей, з якими ці значення набуваються, будемо використовувати теорему множення ймовірностей для незалежних подій. Отже, загальна формула визначення відповідних імовірностей буде такою:
= k, ... Для знаходження ймовірностей, з якими ці значення набуваються, будемо використовувати теорему множення ймовірностей для незалежних подій. Отже, загальна формула визначення відповідних імовірностей буде такою:
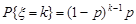 , де р = 0,2, k = 1, 2, ... .
, де р = 0,2, k = 1, 2, ... .
Таким чином, ряд розподілу 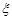 має вигляд (табл.9.2):
має вигляд (табл.9.2):
Таблиця 9.2
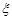
| ... | k | ... | ||
| р | 0,2 | 0,16 | ... | 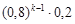
| ... |
Дата добавления: 2016-11-02; просмотров: 993;
