Функція розподілу випадкової величини
Та її властивості
Ряд розподілу дискретної випадкової величини 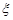 є повною ймовірнісною характеристикою цієї величини. Але дискретними випадковими величинами не вичерпуються всі види випадкових величин. Наприклад, ряд розподілу не підходить для опису випадкових величин, які набувають незліченної множини значень. Необхідно ввести універсальну ймовірнісну характеристику, яка годиться для опису будь-якої випадкової величини. Такою характеристикою є функція розподілу випадкової величини.
є повною ймовірнісною характеристикою цієї величини. Але дискретними випадковими величинами не вичерпуються всі види випадкових величин. Наприклад, ряд розподілу не підходить для опису випадкових величин, які набувають незліченної множини значень. Необхідно ввести універсальну ймовірнісну характеристику, яка годиться для опису будь-якої випадкової величини. Такою характеристикою є функція розподілу випадкової величини.
Означення 9.4. Функція 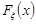 дійсної змінної
дійсної змінної 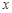 , значення якої при кожному значенні аргументу дорівнює ймовірності події
, значення якої при кожному значенні аргументу дорівнює ймовірності події 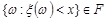 , тобто
, тобто
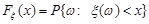 , (9.1)
, (9.1)
називається функцією розподілу випадкової величини 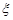 .
.
Іноді функцію розподілу називають інтегральним законом розподілу випадкової величини.
Наведемо властивості функції розподілу випадкової величини.
1. Функція розподілу 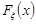 випадкової величини
випадкової величини 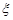 є монотонно неспадна функція.
є монотонно неспадна функція.
Доведення. Для будь-яких 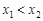 випадкова подія
випадкова подія 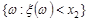 включає подію
включає подію 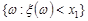 , тоді з властивості 4 ймовірності (лекція 4) випливає
, тоді з властивості 4 ймовірності (лекція 4) випливає 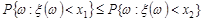 . Користуючись означенням 9.4, маємо
. Користуючись означенням 9.4, маємо 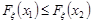 .
.
2. 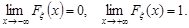
Доведення. Розглянемо дві числові послідовності 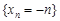 та
та 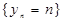 . Введемо позначення
. Введемо позначення 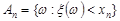 та
та 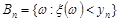 . Послідовність випадкових подій
. Послідовність випадкових подій 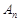 буде монотонно спадною послідовність і
буде монотонно спадною послідовність і 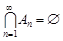 . За аксіомою неперервності маємо
. За аксіомою неперервності маємо
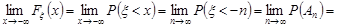
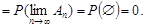
Послідовність випадкових подій 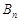 – монотонно зростаюча, крім того,
– монотонно зростаюча, крім того, 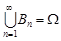 , тому
, тому
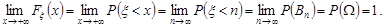
3. Функція розподілу 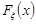 випадкової величини
випадкової величини 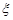 є неперервною зліва, тобто
є неперервною зліва, тобто 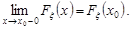
Доведення. Нехай числова послідовність 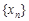 – монотонно зростаюча і
– монотонно зростаюча і 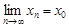 . Введемо випадкові події:
. Введемо випадкові події: 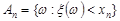 і
і 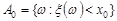 . Тоді
. Тоді 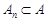 і послідовність подій
і послідовність подій 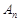 “розширюється” до
“розширюється” до 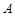 . Отже,
. Отже, 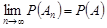 . Враховуючи властивість 1 функції розподілу, маємо
. Враховуючи властивість 1 функції розподілу, маємо
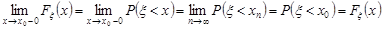 .
.
Зауваження. Якщо функцію розподілу визначити як 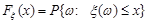 , то при такому означенні вона буде неперервною справа.
, то при такому означенні вона буде неперервною справа.
4. Область значень функції розподілу є проміжок 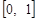 .
.
Ця властивість випливає безпосередньо з означення 9.4.
5. Імовірність попадання випадкової величини 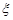 в проміжок
в проміжок 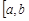 ) можна обчислити за формулою
) можна обчислити за формулою
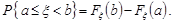 (9.2)
(9.2)
Доведення. Введемо випадкові події 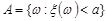 ,
, 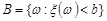 і
і 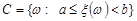 , тоді подія
, тоді подія 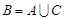 , причому
, причому  . За аксіомою скінченої адитивності ймовірності
. За аксіомою скінченої адитивності ймовірності
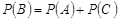 або
або 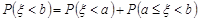 .
.
Звідки
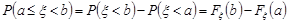 .
.
6. В якості проміжку 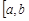 ) розглянемо елементарний проміжок
) розглянемо елементарний проміжок 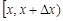 і застосуємо до нього формулу (9.2), тоді
і застосуємо до нього формулу (9.2), тоді
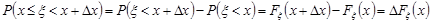 Звідси випливає
Звідси випливає
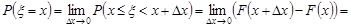
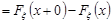 .
.
Отже, якщо x – точка неперервності функції розподілу, то 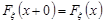 і ймовірність
і ймовірність 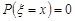 . Якщо x – точка розриву функції розподілу, то ймовірність події
. Якщо x – точка розриву функції розподілу, то ймовірність події 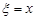 дорівнює величині стрибка функції розподілу в цій точці.
дорівнює величині стрибка функції розподілу в цій точці.
Нехай випадкова величина 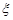 – дискретна,
– дискретна, 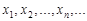 – її можливі значення. Тоді в кожній точці
– її можливі значення. Тоді в кожній точці 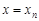 (n=1, 2, …) її функція розподілу має стрибки, величина яких дорівнює
(n=1, 2, …) її функція розподілу має стрибки, величина яких дорівнює 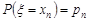
(n= 1, 2, …). Таким чином, функція розподілу дискретної випадкової величини 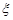 завжди розривна, має скінчену або злічену кількість стрибків у точках можливих значень випадкової величини. У загальному вигляді її можна записати так:
завжди розривна, має скінчену або злічену кількість стрибків у точках можливих значень випадкової величини. У загальному вигляді її можна записати так:
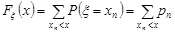 . (9.3)
. (9.3)
Нехай тепер функція розподілу 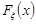 деякої випадкової величини – неперервна. Це означає, що ймовірність події
деякої випадкової величини – неперервна. Це означає, що ймовірність події 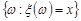 дорівнює нуля для всіх
дорівнює нуля для всіх 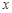 , тобто кожне окремо взяте значення не має додатної ймовірності. У цьому випадку можливі значення випадкової величини
, тобто кожне окремо взяте значення не має додатної ймовірності. У цьому випадку можливі значення випадкової величини 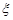 повністю заповнюють деякий проміжок, а, можливо, і всю числову вісь.
повністю заповнюють деякий проміжок, а, можливо, і всю числову вісь.
Розглянемо на прикладі побудову графіка функції розподілу дискретної випадкової величини.
Приклад 9.2. Три рази стріляють по мішені. Імовірність влучення при кожному пострілі дорівнює 0,3. Нехай випадкова величина 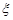 означає кількість влучень при трьох пострілах. Треба:
означає кількість влучень при трьох пострілах. Треба:
1) скласти ряд розподілу випадкової величини 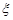 ;
;
2) записати і побудувати графік функції розподілу;
3) знайти ймовірність події А ={кількість влучень буде не менше двох}.
Розв’язання. 1. При складанні ряду розподілу необхідно знати значення 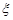 та ймовірності p, з якими ці значення набуваються. За умовою задачі
та ймовірності p, з якими ці значення набуваються. За умовою задачі 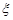 може набувати чотирьох значень:
може набувати чотирьох значень: 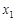 = 0,
= 0, 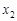 = 1,
= 1, 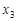 = 2,
= 2, 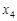 = 3. Імовірності, з якими ці значення набуваються, знайдемо за формулою Бернуллі:
= 3. Імовірності, з якими ці значення набуваються, знайдемо за формулою Бернуллі:
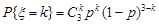 , де k = 0, 1, 2, 3; p = 0,3.
, де k = 0, 1, 2, 3; p = 0,3.
Отже, ряд розподілу випадкової величини 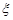 має вигляд (табл.9.3):
має вигляд (табл.9.3):
Таблиця 9.3
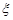
| ||||
| p | 0,343 | 0,441 | 0,189 | 0,027 |
2. Записуємо функцію розподілу, користуючись рядом розподілу:
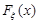 =
= 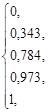
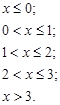
Графік функції розподілу наведений на рис. 9.1.
 |
Рис. 9.1
3. Імовірність події А знайдемо за формулою (9.2):
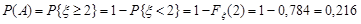 .
.
Дата добавления: 2016-11-02; просмотров: 1671;
