Означення та приклади випадкових величин
Випадкова подія є якісною характеристикою 
можливого результату стохастичного експерименту. Для успішного використання методів математичного аналізу в розв’язанні проблем теорії ймовірностей необхідно ввести кількісну характеристику випадкового результату стохастичного експерименту. Такою характеристикою є випадкова величина – одне з основних понять теорії ймовірностей. Наведемо строге математичне означення випадкової величини.
Означення 9.1. Нехай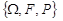 
– ймовірнісний простір стохастичного експерименту. Функція 
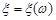, яка визначена на просторі W, має значення у множині дійсних чисел R і для 
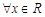– подія 
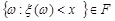, називається випадковою величиною.
Функції, які задовольняють цим умовам, у теорії функцій називаються вимірнимифункціями відносно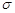 
- алгебри F. Отже, можна сказати, що випадкова величина – це дійснозначна функція, яка задана на ймовірнісному просторі, вимірна відносно 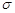- алгебри F. Властивість вимірності випадкової величини потрібна для того, щоб мати можливість знаходити ймовірності подій вигляду 
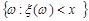. Можна довести, що з того, що 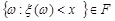випливає, що події вигляду
, 
, 
, 
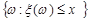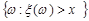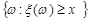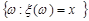
також належать 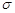- алгебрі F.
Традиційно аргумент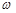 
у позначенні випадкової величини опускають і позначають випадкові величини літерами грецького алфавіту 
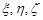, а їх можливі значення літерами латинського алфавіту 
.
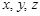Наведемо деякі приклади випадкових величин: 1) кількість очок, які випали при киданні грального кубика; 2) кількість влучень у мішень при n пострілах; 3) час безвідмовної роботи приладів; 4) помилки вимірювань; 5) тривалість життя біологічної особі тощо. Вже ці приклади показують наскільки можуть бути різноманітними випадкові величини. Для того, щоб їх вивчення було послідовним і систематизованим, випадкові величини поділяють в основному на два класи: дискретні та неперервні випадкові величини.
Дата добавления: 2016-11-02; просмотров: 598;