Функція розподілу двовимірного випадкового вектора
Та її властивості.
Функція розподілу випадкового вектора, як і для випадкових величин, є повною імовірнісною характеристикою вектора. Для кращого розуміння властивостей функції розподілу випадкового вектора розглянемо випадок системи двох випадкових величин.
Означення 14.3. Функцією розподілу випадкового вектора 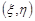 називається ймовірність одночасної появи двох подій
називається ймовірність одночасної появи двох подій 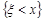 та
та 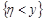 , де
, де 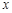 та
та 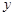 – будь-які дійсні числа, тобто
– будь-які дійсні числа, тобто
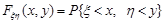 . (14.3)
. (14.3)
Функція розподілу двовимірного випадкового вектора має просту геометричну інтерпретацію: значення 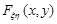 збігаються з імовірністю попадання точки з випадковими координатами системи
збігаються з імовірністю попадання точки з випадковими координатами системи 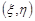 усередину нескінченного квадранта з вершиною у точці
усередину нескінченного квадранта з вершиною у точці 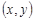 (рис. 14.1).
(рис. 14.1).
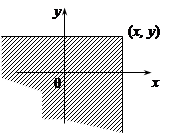 |
Рис. 14.1
Наведемо властивості функції розподілу 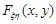 .
.
1. Функція розподілу є монотонно неспадною функцією двох аргументів, область зміни якої є відрізок 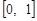 .
.
Доведення. Треба довести, що 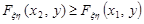 , якщо
, якщо 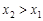 або
або 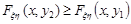 , якщо
, якщо 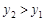 . Доведемо, наприклад, перше твердження. Введемо події
. Доведемо, наприклад, перше твердження. Введемо події 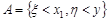 ,
, 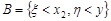 ,
, 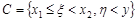 . Ці події несумісні, причому
. Ці події несумісні, причому 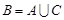 . Отже,
. Отже, 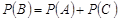 , тобто
, тобто
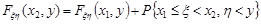 .
.
Звідки випливає 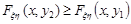 , бо
, бо 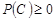 . Аналогічно довести друге твердження.
. Аналогічно довести друге твердження.
2. 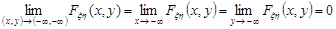 .
.
Доведення. Доведемо, наприклад, що 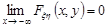 . Інші співвідношення доводяться аналогічно.
. Інші співвідношення доводяться аналогічно.
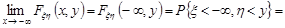
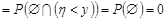 .
.
3. Мають місце умови узгодженості:
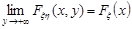 ,
, 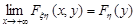 .
.
Доведення. Доведемо справедливість першої рівності.
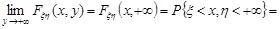
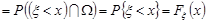 .
.
Властивість 3 показує, що за двовимірним законом розподілу завжди можна знайти закони розподілу окремих компонент випадкового вектора.
4. 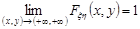 .
.
Властивість доводиться аналогічно попереднім властивостям.
5. Функція розподілу системи двох випадкових величин є неперервною зліва по кожному з аргументів, тобто
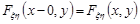 і
і 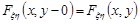 .
.
Властивість доводиться аналогічно властивості неперервності зліва функції розподілу випадкової величини.
6. Імовірність попадання випадкової точки 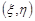 в прямокутник
в прямокутник 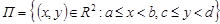 дорівнює
дорівнює
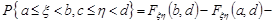
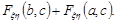
Доведення.
Введемо події: 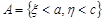 ,
, 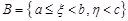 ,
, 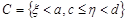 ,
, 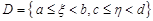 ,
, 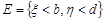 . Неважко зрозуміти, що ці події попарно несумісні і
. Неважко зрозуміти, що ці події попарно несумісні і 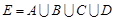 . За аксіомою скінченої адитивності ймовірностей
. За аксіомою скінченої адитивності ймовірностей 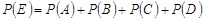 , звідки
, звідки
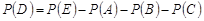 .
.
Врахуємо, що
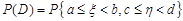 ,
, 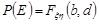 ,
,
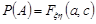 ,
, 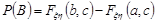 ,
,
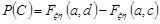 .
.
Остаточно
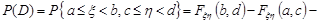
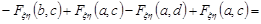
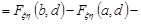
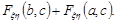
Для дискретного двовимірного випадкового вектора функція розподілу записується коротко так: 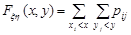 .
.
Приклад 14.2. Зроблено три постріли по мішені. Імовірність влучення при кожному пострілі дорівнює 0,4. Для ураження мішені достатньо двох влучень, а при одному влученні мішень може бути уражена з імовірністю, яка дорівнює 0,8.
1. Скласти таблицю розподілу випадкового вектора 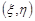 , де
, де 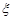 – загальне число влучень,
– загальне число влучень, 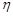 характеризує стан мішені, тобто
характеризує стан мішені, тобто 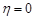 , якщо мішень не уражена та
, якщо мішень не уражена та 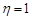 , якщо мішень уражена.
, якщо мішень уражена.
2. Записати функцію розподілу системи випадкових величин 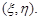
3. Знайти ймовірність події 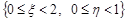 .
.
Розв’язання.
1. Імовірність 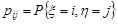 , i=0, 1, 2, 3; j=0, 1. Знайдемо значення
, i=0, 1, 2, 3; j=0, 1. Знайдемо значення 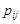 за теоремою множення ймовірностей та формулою Бернуллі:
за теоремою множення ймовірностей та формулою Бернуллі:
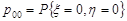 =
= 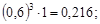
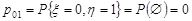 ;
;
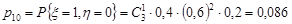 ;
;
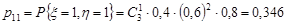 ;
;
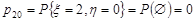 ;
;
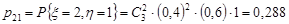 ;
;
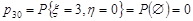 ;
;
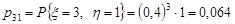 .
.
Зробимо перевірку результатів:
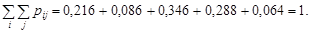
Складемо таблицю розподілу системи 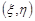 (табл.14.3).
(табл.14.3).
Таблиця 14.3
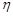
| 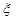
| |||
| 0,216 | 0,086 | |||
| 0,346 | 0,288 | 0,064 |
2. Для знаходження функції розподілу 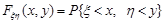 зручно використовувати її геометричну інтерпретацію, оскільки значення
зручно використовувати її геометричну інтерпретацію, оскільки значення 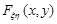 збігаються з імовірністю попадання точки з випадковими координатами системи
збігаються з імовірністю попадання точки з випадковими координатами системи 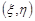 усередину нескінченного квадранта з вершиною у точці
усередину нескінченного квадранта з вершиною у точці 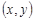 (рис. 14.1).
(рис. 14.1).
Систему випадкових величин 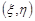 можна зобразити вісьмома точками на площині XOY. При
можна зобразити вісьмома точками на площині XOY. При 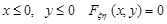 . Дійсно, у цьому випадку в зазначеній області немає жодної точки можливих значень
. Дійсно, у цьому випадку в зазначеній області немає жодної точки можливих значень 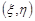 (рис. 14.2).
(рис. 14.2).
 |
Рис.14.2
При 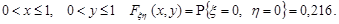 Дійсно, в заштрихованій на рис. 14.3 області знаходиться точка з координатами (0,0).
Дійсно, в заштрихованій на рис. 14.3 області знаходиться точка з координатами (0,0).
При 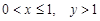
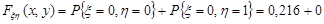 (рис. 14.4).
(рис. 14.4).
 |
Рис. 14.3 Рис. 14.4
Аналогічно, орієнтуючись весь час на геометричну інтерпретацію функції розподілу, знаходимо всі значення 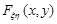 . Відшукані значення заносимо в таблицю (табл. 14.4).
. Відшукані значення заносимо в таблицю (табл. 14.4).
Таблиця 14.4
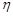
| 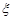
| ||||
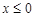
| 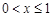
| 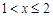
| 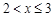
| 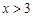
| |
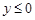
| |||||
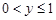
| 0,216 | 0,302 | 0,302 | 0,302 | |
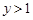
| 0,216 | 0,648 | 0,936 | 1,000 |
3. Для знаходження ймовірності події 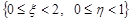 скористуємося властивістю 6 функції розподілу. Відповідні значення функції розподілу візьмемо з таблиці. Отже,
скористуємося властивістю 6 функції розподілу. Відповідні значення функції розподілу візьмемо з таблиці. Отже,
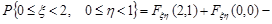
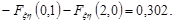
Дата добавления: 2016-11-02; просмотров: 1393;
