Визначення, позначення, загальні відомості
ЧИСЛОВЕ РОЗВ’ЯЗАННЯ СИСТЕМ АЛГЕБРАЇЧНИХ
РІВНЯНЬ
Визначення, позначення, загальні відомості
Успішне рішення більшості науково-технічних задач в значному ступені залежить від уміння швидко і точно розв’язувати системи лінійних алгебраїчних рівнянь. Багато методів розв’язання нелінійних задач також зводиться до розв’язання деякої послідовності лінійних систем. Зараз розроблено достатньо числових методів розв’язання лінійних алгебраїчних рівнянь на ЕОМ. Для багатьох методів розроблено математичний апарат, який дозволяє оцінювати точність отриманого рішення і визначити кількість вірних знаків розрахованого на ЕОМ рішення. Числові методи розв’язання лінійних алгебраїчних систем можна розділити на прямі (точні) та ітераційні.
Прямі методи характеризуються тим, що дають розв’язання за скінченну кількість арифметичних операцій. Якщо всі операції виконуються точно (без похибок округлення), то розв’язання заданої системи також виходить точним. До прямих методів відносяться: метод Крамера, методи послідовного виключення невідомих (метод Гауса та його модифікації, метод квадратного кореня, метод відображення та інші), метод ортогоналізації. Прямі методи застосовуються на практиці для розв’язання систем на ЕОМ, як правило, з числами не віще 103.
Ітераційні методи є наближеними. Вони дають розв’язання системи як межу послідовних наближень, що розраховуються за однаковою схемою. До ітераційних методів відносяться: метод простої ітерації, метод Зейделя, метод релаксацій, градієнтні методи та їх модифікації. На практиці ітераційні методи застосовуються для розв’язання з числами порядку 106.
Розглянемо деякі відомості з теорії матриць. Прямокутна таблиця, яка складається з елементів (в окремому випадку чисел) і має m рядків і n стовпців, називається матрицею типу 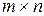 .
.
Наприклад,

матриця 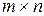 , яка має m рядків і n стовпців
, яка має m рядків і n стовпців
Зазначимо, що скорочений запис матриці 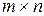 має вигляд
має вигляд 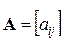 , де і = 1, 2, …, m; j = 1, 2, …, n.
, де і = 1, 2, …, m; j = 1, 2, …, n.
Якщо в матриці 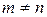 , тобто кількість рядків не дорівнює кількості стовпців, то матриця називається прямокутною.
, тобто кількість рядків не дорівнює кількості стовпців, то матриця називається прямокутною.
Матриця, яка має тільки один рядок, тобто m = 1, називається матрицею-рядком або вектором-рядком, наприклад,
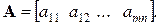
Матриця, яка має тільки один стовпчик, тобто 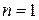 , називається матрицею-стовпчиком або вектором-стовпчиком, наприклад,
, називається матрицею-стовпчиком або вектором-стовпчиком, наприклад,
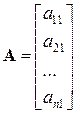 .
.
Матриця АТ, яка отримана перестановкою в матриці А рядків зі стовбцями, називається транспонованою матрицею
 .
.
Приклад 1. Для матриці

типу  транспонованою матрицею буде матриця
транспонованою матрицею буде матриця
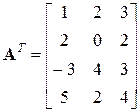
типу 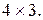
Транспонування матриці-стовпця дає матрицю-рядок, і навпаки.
Матриця, в якій кількість рядків дорівнює кількості стовпчиків, тобто 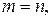 називається квадратною. Таку матрицю можна записати у вигляді
називається квадратною. Таку матрицю можна записати у вигляді
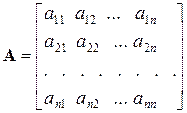 .
.
Для квадратної матриці загальна кількість рядків або стовпчиків називається порядком матриці.
Головною діагоналлю квадратної матриці називається діагональ, що проходить через верхній лівий і нижній правий кути, тобто це є сукупність елементів вигляду аіі, де і = 1, 2, …, n.
Квадратна матриця, в якій всі елементи, що розташовані зовні головної діагоналі, дорівнюють нулю, називається діагональною. Така матриця має вигляд
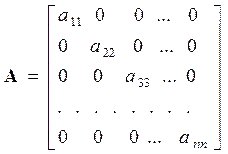
Діагональна матриця, в якій всі елементи, що розташовані на головній діагоналі, дорівнюють одиниці. Одиночна матриця позначається літерою Е і має вигляд
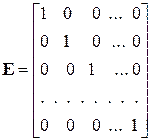 .
.
У матричному численні одинична матриця грає роль одиниці.
Матриця, всі елементи якої дорівнюють нулю, називається нульовою і позначається літерою О.
Квадратна матриця, в якій всі елементи розташовані симетрично відносно головної діагоналі, називається симетричною. Для симетричної матриці має місце рівність 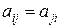 .
.
Визначник матриці
З квадратною матрицею пов’язаний визначник (детермінант), який позначається 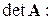
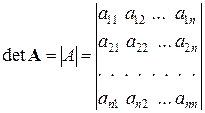 .
.
У визначнику розрізняють дві діагоналі: головну та побічну. Головна діагональ складається з елементів аіі, де і = 1, 2, …, n.
Побічна діагональ проходить перпендикулярно до головної, тобто з верхнього правого кута визначника в нижній лівий кут.
Якщо матриця А квадратна та її визначник не дорівнює нулю 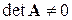 , то вона називається неособливою (невиродженою).
, то вона називається неособливою (невиродженою).
Для неособливої матриці важливим є поняття оберненої матриці. Оберненою по відношенню до даної називається матриця А–1, яка, будучи помноженою як справа, так і зліва на вказану матрицю, дає одиничну матрицю, тобто
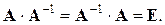
Матриця називається ортогональною, якщо сума квадратів елементів кожного стовбцю дорівнює одиниці, а сума добутків відповідних елементів двох різних стовбців дорівнює нулю, тобто

Визначник другого порядку дорівнює добутку елементів головної діагоналі мінус добуток елементів побічної діагоналі

Визначником третього порядку є число
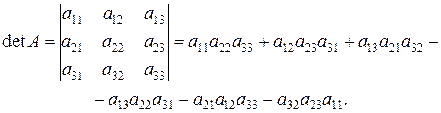
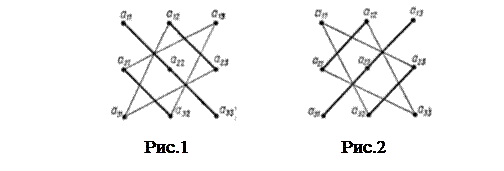 |
Таким чином, кожний член визначника третього порядку є добутком трьох його елементів, взятих по одному з кожного його рядка та кожного стовпця. Ці добутки беруться з визначеними знаками: зі знаком плюс – три члени, що складаються з елементів головної діагоналі та з елементів, розташованих у вершинах рівнобедрених трикутників з основами, паралельними головній діагоналі (рис. 1); зі знаком мінус – три члени, розташовані аналогічним чином відносно побічної діагоналі (рис. 2). Це правило називається правилом трикутників.
Властивості визначників.
1. Визначник не змінюється при транспонуванні:
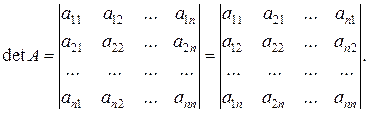
2. Якщо один із рядків або один із стовпців визначника складається з нулів, то визначник дорівнює нулю.
3. Від перестановки двох рядків або двох стовпців визначник змінює тільки знак.
4. Визначник, що містить два однакових рядки або два однакових стовпця, дорівнює нулю.
5. Якщо всі елементи деякого рядка або стовпця визначника помножити на число 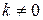 , то сам визначник буде помножений на це число.
, то сам визначник буде помножений на це число.
6. Визначник, що містить два пропорційні рядки, дорівнює нулю.
Застосовуючи властивості визначників, можна спростити задачу обчислення визначників n-го порядку.
Визначник n-го порядку може бути виражений через визначники більш низьких порядків.
Дата добавления: 2016-11-02; просмотров: 1691;
