Системи лінійних алгебраїчних рівнянь
Розглянемо систему m лінійних алгебраїчних рівнянь n з невідомими:
 (1)
(1)
яка може бути записана в матричному вигляді
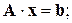
де
 –
–
прямокутна матриця розмірності 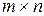 , яка має m рядків і n стовпчиків,
, яка має m рядків і n стовпчиків,
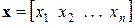 – вектор-рядок n-го порядку, який отримують із матриці
– вектор-рядок n-го порядку, який отримують із матриці 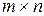 при m = 1;
при m = 1;
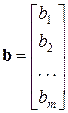 – вектор-стовпчик m-го порядку, який також отримують із матриці
– вектор-стовпчик m-го порядку, який також отримують із матриці 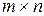 при n = 1.
при n = 1.
Матриця
 ,
,
яка отримана з матриці А додаванням стовбцю вільних членів, називається розширеною.
Розв’язанням системи (1) називається така упорядкована сукупність чисел 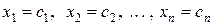 , яка обертає всі рівняння системи в вірні рівності.
, яка обертає всі рівняння системи в вірні рівності.
Система лінійних рівнянь називається сумісною, якщо вона має хоча б одне рішення, і несумісною (суперечливою), якщо вона не має рішень.
Сумісна система називається визначеною, якщо вона має єдине рішення, невизначеною, якщо існує більше одного рішення.
Дві системи лінійних рівнянь називаються рівносильними (еквівалентними), якщо кожне рішення першою системи є рішенням другої системи, і навпаки.
Система лінійних алгебраїчних з n невідомими, яка має неособливу матрицю А, сумісна і має єдине рішення.
Класи задач, для яких застосовуються методі розв’язання систем лінійних алгебраїчних рівнянь, можна умовно назвати, відповідно, до класів задач з малою, середньою і великою кількістю невідомих.
Зазначимо, що результати навіть точних методів є наближеними, що обумовлюється неминучим округленням вихідних даних і проміжних обчислень. При застосуванні ітераційних методів окрім похибки округлення виникає і похибка методу.
Метод Гауса
Найбільш відомим із точних методів розв’язання систем лінійних алгебраїчних рівнянь є метод виключення Гауса.
Більшість поширених точних методів можна розглядати як варіанти методу Гауса, які різняться між собою деякими деталями.
У загальному випадку система рівнянь, яка передбачається не виродженою, має вигляд:
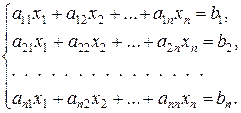 (2)
(2)
Метод Гауса розв’язання системи (2) – це метод послідовного виключення невідомих. Суть його полягає в перетворенні системи (2) до еквівалентної системи, що має вигляд трикутної матриці (прямий хід), із якої потім послідовно (зворотним ходом) розраховують значення всіх невідомих.
Відмінність визначника системи від нуля є необхідною та достатньою умовою існування єдиного рішення системи (2). Якщо визначник системи дорівнює нулю, то система або не має рішення, або має безліч рішень.
Якщо визначник системи близький до нуля, кажуть, що система погано обумовлена. В подібному випадку знайти числове рішення системи важко, а його точність сумнівна.
Розглянемо загальну схему методу Гауса для систем, які мають єдине рішення.
Припустимо, що 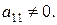 У протилежному випадку можна поміняти місцями перше рівняння з рівнянням, в якому коефіцієнт при х1 відмінний від нуля. Розділимо перше рівняння (2) на а11. Воно прийме вигляд
У протилежному випадку можна поміняти місцями перше рівняння з рівнянням, в якому коефіцієнт при х1 відмінний від нуля. Розділимо перше рівняння (2) на а11. Воно прийме вигляд
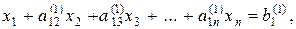 (3)
(3)
де 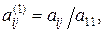
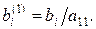
Помножимо рівняння (3) на а21 і віднімемо отримане рівняння із другого рівняння системи (2). Аналогічно перетворимо інші рівняння. В результаті цих операцій система рівнянь набуде вигляду:
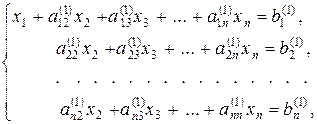 (4)
(4)
де 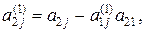
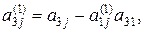 …,
…,
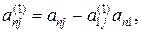
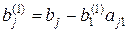
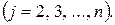
У випадку, коли деякий з коефіцієнтів 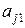 виявиться рівним нулю, то j-е рівняння системи (2) увійде до системи (4) без зміни, тобто
виявиться рівним нулю, то j-е рівняння системи (2) увійде до системи (4) без зміни, тобто 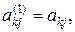
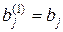
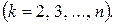 .
.
Тепер, залишивши без зміни перше рівняння системи (4), можна взяти за основу друге рівняння і застосувати описану процедуру до системи з (n – 1) рівнянь, виключивши невідоме х2 з третього та наступних рівнянь. Отримаємо систему наступного вигляду
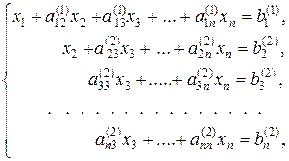 (4)
(4)
де 
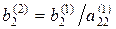 ,
, 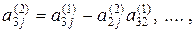
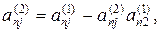
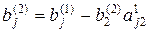
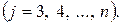
Продовжуючи аналогічні перетворення, приводимо матицю (2) до еквівалентної системи
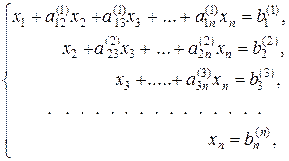 (5)
(5)
в якій матриця із коефіцієнтів має трикутний вигляд.
На цьому прямий хід розв’язання системи лінійних рівнянь методом Гауса закінчується.
При оберненому ході відбувається послідовне виключення невідомого xn , починаючи з (n – 1)-го рівняння. Отримуємо
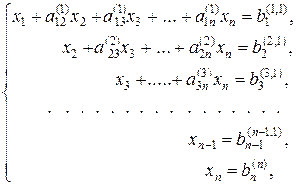
Для зменшення похибки обчислень існують різні модифікації методу Гауса. Одна із модифікацій методу Гауса з вибором максимального елемента по стовпцю полягає в наступному.
На початку першого кроку прямого ходу серед коефіцієнтів аі1 (і = 1, 2, …, n) при невідомому х1 знаходять найбільший за модулем. Припустимо, що це аj1. Після цього в системі рівнянь (2) виконують перестановку: перше рівняння ставлять на місце j-го, а j-е на місце першого. Далі обчислення проводять в послідовності, описаній вище.
На початку другого кроку прямого ходу максимальний за модулем елемент вибирають серед коефіцієнтів аі2 (і = 2, 3, …, n) при невідомому х2, знову можлива відповідна перестановка та виключення невідомого х2, починаючи з третього рівняння, і аж до останнього кроку прямого ходу в методі Гауса.
Зауважимо, що процедура прямого ходу в методі Гауса може призвести не до трикутної матриці (5), а до двох випадків:
1) кількість перетворених рівнянь системи менше кількості невідомих (це відбувається, якщо в процесі перетворень отримується тотожність 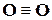 ) – тоді система має нескінченну множину рішень;
) – тоді система має нескінченну множину рішень;
2) всі коефіцієнти при невідомих в якомусь рівнянні дорівнюють нулю, в той же час як вільний член рівняння відрізняється від нуля – тоді система не має рішення.
Метод ітерацій
Розглянемо систему лінійних алгебраїчних рівнянь
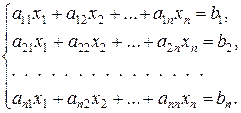 (6)
(6)
Якщо всі діагональні коефіцієнти 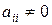 (і = 1, 2, …, n), то систему (6) можна подати в так званому приведеному вигляді
(і = 1, 2, …, n), то систему (6) можна подати в так званому приведеному вигляді
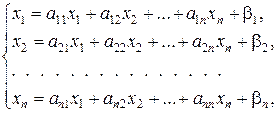 (7)
(7)
де 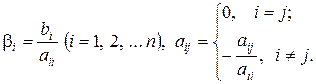
Введемо позначення

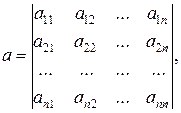
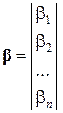
и перепишемо систему (7) у вигляді єдиного матричного рівняння
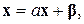 (8)
(8)
де 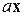 добуток матриці а на вектор х.
добуток матриці а на вектор х.
Послідовні наближення (ітерації) знаходимо наступним чином. Візьмемо за початкове наближення х(0) вектор β і підставимо його в праву частину (8); отримуємо х(1). Продовжуючи аналогічні обчислення, приходимо до векторної послідовності наближень
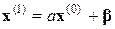 – перше наближення,
– перше наближення,
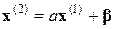 – друге наближення,
– друге наближення,
……………… (9)
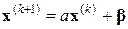 – (k + 1)-е наближення.
– (k + 1)-е наближення.
……………………………………………
Якщо існує границя ξ послідовності векторів 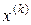 , то переходячи до границі в рівності
, то переходячи до границі в рівності 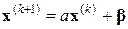 при
при 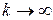 , переконуємося, що ξ є рішенням рівняння (8), тобто
, переконуємося, що ξ є рішенням рівняння (8), тобто
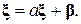
Достатньою умовою збіжності ітерацій до рішення є наступна теорема.
Теорема. Якщо будь-яка норма матриці менше одиниці  , то рівняння (8) має єдине рішення ξ, до якого прагне послідовність ітерацій при будь-якому виборі початкового наближення х(0).
, то рівняння (8) має єдине рішення ξ, до якого прагне послідовність ітерацій при будь-якому виборі початкового наближення х(0).
Метод Зейделя
Метод Зейделя є деякою модифікацією методу послідовних наближень. Знову розглянемо систему лінійних рівнянь (1) та еквіваленту їй приведену систему (7). При розв’язанні системи (7) методом простої ітерації кожний крок складається в переході від вже існуючого наближення значень невідомих до нового (чергового) наближення. В методі Зейделя при розрахунку (k + 1)-го наближення невідомого хі враховуються вже знайдені раніше (k + 1)-е наближення невідомих х1, х2, …, хn.
Для розв’язання системи (1) вибираємо довільне початкове наближення коренів 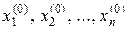 і підставляємо в перше рівняння системи (1):
і підставляємо в перше рівняння системи (1):

отримане перше наближення 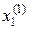 підставляємо до другого рівняння системи (7)
підставляємо до другого рівняння системи (7)
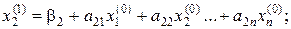
отримані перші наближення 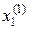 і
і  підставляємо до третього рівняння системи (7)
підставляємо до третього рівняння системи (7)

і т. д. Нарешті
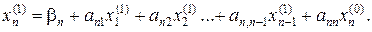
Аналогічно будують другі, треті і т. д. ітерації.
Таким чином, передбачаючи, що k-е наближення коренів 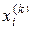 відомі, за методом Зейделя будуємо (k + 1)-е наближення за наступними формулами
відомі, за методом Зейделя будуємо (k + 1)-е наближення за наступними формулами

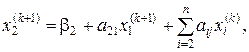
………………………………….
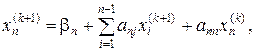
де 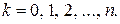
Дата добавления: 2016-11-02; просмотров: 1571;
