Генератриса та її використання при вивченні дискретних цілочислових невід’ємних випадкових величин
Для вивчення цілочислових дискретних випадкових величин зручно застосовувати поняття генератриси. Наведемо означення.
Означення 12.1. Нехай 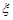 – дискретна випадкова величини, яка набуває тільки цілі невід’ємні значення та має розподіл
– дискретна випадкова величини, яка набуває тільки цілі невід’ємні значення та має розподіл 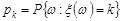 , k = 1,2,... . Функція комплексного змінного
, k = 1,2,... . Функція комплексного змінного 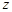 вигляду
вигляду
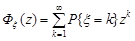 (12.1)
(12.1)
називається генератрисою цієї випадкової величини.
Генератриса має такі властивості.
1. Генератриса є аналітичною функцією в колі 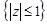 .
.
Дійсно, степеневий ряд (12.1) рівномірно збігається в колі 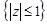 , оскільки мажорується збіжним числовим рядом
, оскільки мажорується збіжним числовим рядом  .
.
2. Генератриса випадкової величини 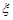 повністю визначає її розподіл.
повністю визначає її розподіл.
Доведення. Генератриса за властивістю 1 є нескінченно диференційовною функцією в колі  , тому коефіцієнти степеневого ряду (12.1) визначаються як коефіцієнти ряду Маклорена, тобто
, тому коефіцієнти степеневого ряду (12.1) визначаються як коефіцієнти ряду Маклорена, тобто
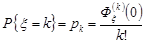 ,
,  .
.
3. Генератриса застосовується для обчислення моментів дискретної цілочислової невід’ємної величини 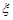 .
.
Зокрема, математичне сподівання та дисперсія випадкових величин обчислюється за формулами:
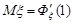 (12.2)
(12.2)
 (12.3)
(12.3)
Доведення.
Оскільки 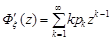 , то
, то  .
.
Знайдемо  .
.
Тоді 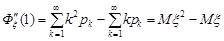 . Звідси
. Звідси
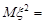
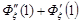 .
.
Остаточно дисперсія дорівнює
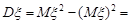
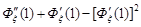 .
.
Аналогічно можна отримати формули для обчислення початкових і центральних моментів дискретної цілочислової випадкової величини будь-якого порядку. Наприклад, 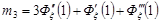 .
.
Генератриса має ще деякі цікаві властивості, які будуть наведені при вивченні характеристичних функцій випадкових величин.
Надалі будемо застосовувати генератрису до вивчення деяких законів розподілу.
12.2. Біномний розподіл (розподіл Бернуллі)
Означення 12.2. Цілочислова невід’ємна випадкова величина 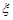 розподілена за біномним законом(законом Бернуллі), якщо подія
розподілена за біномним законом(законом Бернуллі), якщо подія 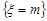 має ймовірність:
має ймовірність:
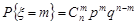 , m = 0, 1, 2,...., n; q = 1 – p. (12.4)
, m = 0, 1, 2,...., n; q = 1 – p. (12.4)
Числа n і p називаються параметрами розподілу. За біномним законом розподілено число появ події А в n незалежних випробуваннях, якщо ймовірність появи події А в кожному випробуванні дорівнює p (схема Бернуллі).
Функція розподілу випадкової величини 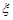 має вигляд:
має вигляд:

Знайдемо за означенням генератрису біномного розподілу.
 .
.
Числові характеристики обчислимо за формулами (12.2) та (12.3). Знайдемо похідні генератриси 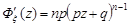 ,
, 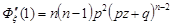 .
.
Звідки
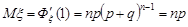 ,
,
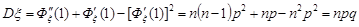 ,
,
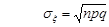 .
.
Приклад 12.1. Знайти ймовірність того, що випадкова величина 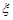 , яка розподілена за законом Бернуллі з параметрами
, яка розподілена за законом Бернуллі з параметрами  , влучить в інтервал [2, 5). Які числові характеристики вона має?
, влучить в інтервал [2, 5). Які числові характеристики вона має?
Розв’язання. Відповідну ймовірність обчислимо за формулою (12.4)
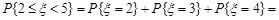
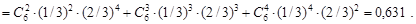
Числові характеристики випадкової величини 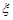 будуть такими: математичне сподівання
будуть такими: математичне сподівання  , дисперсія
, дисперсія 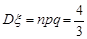 .
.
Дата добавления: 2016-11-02; просмотров: 1893;
