Геометричний розподіл

Означення 12.3. Цілочислова невід’ємна випадкова величина 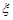розподілена за геометричним законом,якщо подія 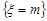має ймовірність:

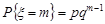, m = 1, 2, ... ; q = 1 – p. (12.5)

Число p є параметр геометричного розподілу.

Геометричний розподіл імовірностей зустрічається в таких задачах. Нехай проводять незалежні випробування до першої появи успіху, причому ймовірність того, що дослід буде успішним дорівнює 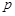. Дискретна випадкова величина 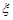, яка задає кількість проведених випробувань у такому експерименті, включаючи успішний, розподілена за геометричним законом.

Функція розподілу геометрично розподіленої випадкової величини 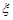має вигляд:

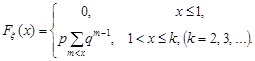
Знайдемо генератрису геометричного розподілу:

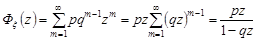при умові, що 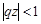. Тоді числові характеристики випадкової величини 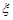обчислюємо за формулами (12.2), (12.3). Перша та друга похідні від генератриси будуть такими:

, .

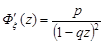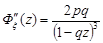Тоді

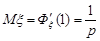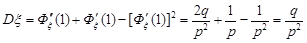Приклад 12.2. Проводять перевірку великої кількості виробів до виявлення бракованого (без обмеження кількості виробів, які перевіряються). Скласти закон розподілу кількості виробів, які перевірили. Знайти його математичне сподівання та дисперсію, якщо ймовірність браку для кожного виробу дорівнює 0,1.

Розв’язання. Дискретна випадкова величина 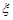– кількість перевірених виробів до виявлення браку має геометричний розподіл з параметром 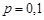. Тому ряд розподілу цієї випадкової величини складаємо, користуючись формулою (12.5).

Таблиця 12.1

( )			_{. . .}		_{. . .}
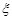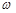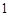
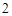
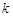
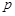
	0,1	0,09	_{. . .}		_{. . .}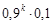

Числові характеристики випадкової величини 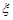будуть такими:

; .

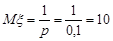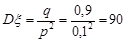Розподіл Пуассона

Означення 12.4. Цілочислова невід’ємна випадкова величина 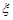розподілена за законом Пуассона,якщо подія 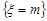має ймовірність:

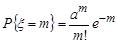, m = 0, 1, 2, ... . (12.6)

Число 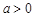є параметр розподілу Пуассона.

Розподіл Пуассона застосовується в теорії випадкових процесів, теорії масового обслуговування, теорії надійності тощо.

Функція розподілу пуассоновської випадкової величини 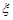має вигляд:

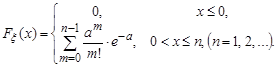
Знайдемо генератрису розподілу Пуассона:

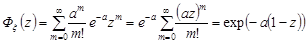Тоді числові характеристики випадкової величини 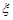обчислюємо за формулами (12.2), (12.3). Перша та друга похідні від генератриси будуть такими:

, .

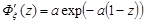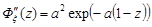Тоді

;

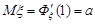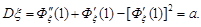
Отже, математичне сподівання та дисперсія пуассоновської випадкової величини 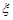дорівнюють параметру а закону Пуассона.

Як приклад застосування закону Пуассона, розглянемо потік подій, який задовольняє певним умовам.

Нехай 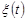– кількість появ деякої події за проміжок часу 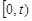. Під потоком подій будемо розуміти послідовність подій, які відбуваються один за одним в певні моменти часу. Припустимо, що потік подій задовольняє таким умовам:

1. Імовірність влучення певної кількості подій за проміжок часу 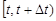залежить тільки від довжини цього проміжку і не залежить від знаходження цього проміжку на вісі часу. Ця умова визначає однорідність потоку подій.

2. Якщо проміжки часу не перетинаються, то кількості подій, які за ці проміжки відбулися, є незалежними подіями. Ця умова називається відсутністю післядії.

3. Імовірність того, що за елементарний час 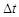з’явиться принаймні одна подія, визначається рівністю

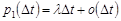, де .

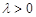Нагадаємо, що 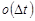є величина вищого порядку малості в порівнянні з 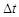, тобто .

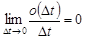4. Імовірність появи більше однієї події за час 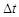дорівнює 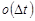, тобто

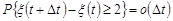Ця умова означає, що події відбуваються поодинці.

Потоки подій, які задовольняють цим умовам, називаються найпростішими потоками.

Для повного ймовірнісного опису таких потоків треба знайти ймовірності подій

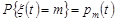, m = 0, 1, 2, … .

Складемо систему диференціальних рівнянь для знаходження ймовірностей .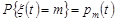

Із умови 2 випливає, що поді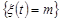ї і 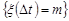є незалежними для всіх m. Тому, ймовірність того, що до моменту часу 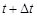відбудеться рівно m подій дорівнює

.

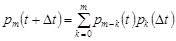Із умов 3 та 4 маємо

.

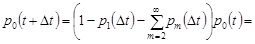
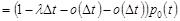Звідси

.

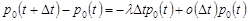Якщо поділити цю рівність на 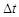та перейти до границі, коли 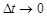, отримаємо

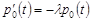. (12.7)

Це диференціальне рівняння дає можливість знайти ймовірність того, що за проміжок часу 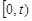не відбудеться жодної події.

Аналогічно для будь-яког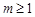о маємо

.

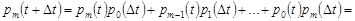
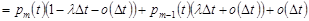Остаточно можна записати

.

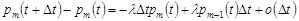Якщо поділити цю рівність на 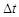та перейти до границі, коли 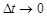, отримаємо

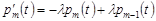, m = 1, 2, … . (12.8)

Система диференціальних рівнянь (12.8) має зліченну множину рівнянь з початковими умовами 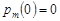, m = 1, 2, … . Розв’язком рівняння (12.7) є функція 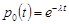, оскільки .

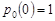Розв’язок системи (12.8) можна знайти звичайними методами інтегрування лінійних диференціальних рівнянь або застосувати операційне числення. Значно простіше отримати розв’язок цієї системи, застосовуючи метод генератрис.

Введемо генератрису ймовірностей :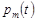

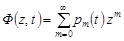. (12.9)

Ряд (12.9) рівномірно збігається в колі 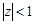і при 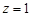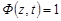. Отже, в середині кола генератрису можна почленно диференціювати. Враховуючи початкові умови, при будь-яких значеннях .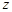

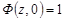Диференціюємо обидві частини (12.9) по t: .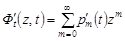

Додамо всі рівняння системи (12.8):

.

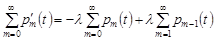Помножимо обидві частини цього рівняння на :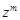

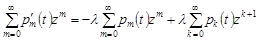, де .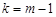

Остаточно

.

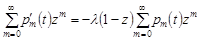Отже, для генератрису маємо таке диференціальне рівняння

,

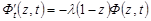загальний інтеграл якого дорівнює

.

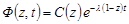Функцію 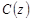визначимо з початкової умови. Оскільки 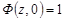, то .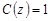

Таким чином, генератриса має вигляд

.

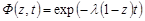Функція такого вигляду є генератриса закону Пуассона з параметром 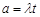. Оскільки, генератриса однозначно визначає розподіл, то ймовірності 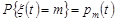дорівнюють

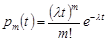, m = 0, 1, 2, … .

Це є розподіл Пуассона з параметром .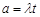

Дата добавления: 2016-11-02; просмотров: 1992;