Кореляційний момент випадкових величин
Означення 1. Кореляційним моментом(кореляцією, коваріацією) K(X,Y) випадкових величин Х та У називається число
K(X,У)= М[(X-MX)(Y-MY)] (9)
Ця величина має розмірність, що дорівнює добутку розмірностей випадкових величин X та У. Скориставшись властивостями математичного сподівання, можна привести формулу (9) до вигляду
К(Х,У) =М(Х  У)-МХ
У)-МХ  МУ. (10)
МУ. (10)
Випадкові величини називаються корельованимипри 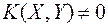 і некорельованимипри
і некорельованимипри
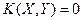 . Якщо випадкові величини незалежні, то із (10) виходить, що
. Якщо випадкові величини незалежні, то із (10) виходить, що 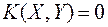 - із незалежності випадкових величин випливає їх некорельованість. Якщо
- із незалежності випадкових величин випливає їх некорельованість. Якщо 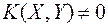 то випадкові величини є залежними -із корельованості випадкових величин випливає їх залежність. Однак, із
то випадкові величини є залежними -із корельованості випадкових величин випливає їх залежність. Однак, із 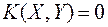 не випливає незалежність випадкових величин - із некорельованості випадкових величин не випливає їх незалежність.
не випливає незалежність випадкових величин - із некорельованості випадкових величин не випливає їх незалежність.
Незалежність 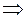 некорельованість некорельованість
|
Корельованість 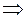 залежність залежність
|
Означення 2. Коефіцієнтом кореляціївипадкових величин Х та У називається число
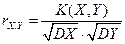 . (11)
. (11)
Приклад 3. Знайти кореляційний момент координат випадкового вектора, заданого таблицею:
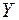
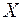
| ||
| 0.3 | 0.5 | |
| 0.1 | 0.1 |
Розв'язання. За формулами (6) знаходимо 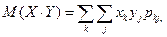 =
=  2
2  0.3+2
0.3+2  2
2  0.5+3
0.5+3  l
l  0.1+ +3
0.1+ +3  2
2  0.1=3.5, MX =2
0.1=3.5, MX =2  0.3+2
0.3+2  0.5+3
0.5+3  0.1+3
0.1+3  0.1=2.2,
0.1=2.2,
МУ =1  0.3+1
0.3+1  0.1+2
0.1+2  0.5+3
0.5+3  0.1=1.6. Тоді за формулою (10) одержимо К(Х,У)=3.5-2.2 1.6= -0.02.
0.1=1.6. Тоді за формулою (10) одержимо К(Х,У)=3.5-2.2 1.6= -0.02.
Регресія
Якщо ми знаємо розподіл однієї координати дискретного випадкового вектора при умові, що інша координата приймає певне значення: 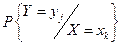 ,
, 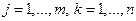 , то можна ввести поняття умовного математичного сподівання.
, то можна ввести поняття умовного математичного сподівання.
Означення 1.Умовним математичним сподіванням 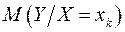 випадкової величини Y при умові, що випадкова величина Х прийняла одно з своїх можливих значень
випадкової величини Y при умові, що випадкова величина Х прийняла одно з своїх можливих значень 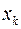 називається число, яке знаходиться за формулою
називається число, яке знаходиться за формулою
 (12)
(12)
Аналогічно визначається умовне математичне сподівання 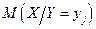 .
.
При зміні х від 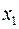 до
до 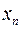 взагалі кажучи, змінюється умовне математичне сподівання
взагалі кажучи, змінюється умовне математичне сподівання 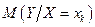 яке можна розглядати у цьому випадку як функцію х:
яке можна розглядати у цьому випадку як функцію х:
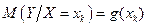 . (13)
. (13)
Ця функція називається регресією У на X (Y відносно X), а її графік 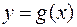 - лінією регресіїY на X. Лінія регресії описує зміну середніх значень випадкової величини У при переході від одного значення Х до іншого.
- лінією регресіїY на X. Лінія регресії описує зміну середніх значень випадкової величини У при переході від одного значення Х до іншого.
Аналогічно визначається регресія Х на У (Х відносно У) і лінія регресії Х на У: 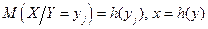 .
.
Для побудови рівняння регресії за означенням (12)-(13) необхідно знати закон розподілу двовимірного випадкового вектора (таблицю з розділа 1.2). На практиці дослідник звичайно має у своєму розпорядженні лише виборку 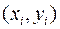 пар чисел скінченного об’єму
пар чисел скінченного об’єму 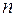 та рівняння регресії визначається методом найменших квадратів (МНК). Доведено, що одержана по МНК функція
та рівняння регресії визначається методом найменших квадратів (МНК). Доведено, що одержана по МНК функція 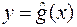 є найкращим наближенням до дійсної лінії регресії
є найкращим наближенням до дійсної лінії регресії 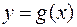 .
.
Випадкові величини X та У називаються лінійно корельованими,якщо лінії регресії є прямими. Рівняння цих прямих такі:
 (У на X) (14)
(У на X) (14)
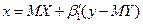 (X на У) (1
(X на У) (1 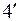 )
)
Якщо лінія регресії У на X (X на У)не є прямою, можна використати першу (другу) із прямих регресії (14)- (1 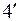 ) в якості наближення до істинної лінії регресії. У цьому випадку ця пряма називається прямою наближеноїрегресії. У зв'язку з цим відзначимо, що функція
) в якості наближення до істинної лінії регресії. У цьому випадку ця пряма називається прямою наближеноїрегресії. У зв'язку з цим відзначимо, що функція 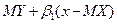 (функція
(функція 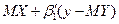 ) єнайкращим наближенням до Y (до X)серед усіх лінійних функцій випадкової величини X (випадкової величини У).
) єнайкращим наближенням до Y (до X)серед усіх лінійних функцій випадкової величини X (випадкової величини У).
Кутові коефіцієнти 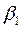 та
та 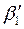 прямих регресії (14)- (1
прямих регресії (14)- (1 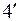 ) називаються відповідно коефіцієнтами регресії У на X та X на У. При цьому
) називаються відповідно коефіцієнтами регресії У на X та X на У. При цьому
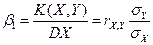 ,
, 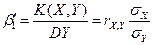 (15)
(15)
Прямі регресії (14)- (1 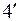 ) проходять через точку з координатами (MX; MY), При
) проходять через точку з координатами (MX; MY), При  прямі регресії співпадають, а при
прямі регресії співпадають, а при 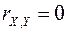 - паралельні осям координат.
- паралельні осям координат.
Приклад 4.Задан закон розподілу дискретного випадкового вектора 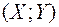 .
.
1. Знайти а) закони розподілу його координат 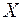 и
и 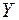 ; б) їх математичні сподівання та дисперсії; в) кореляційний момент
; б) їх математичні сподівання та дисперсії; в) кореляційний момент 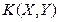 ; г) коефіціент кореляції
; г) коефіціент кореляції 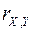 .
.
2. Знайти умовні розподіли 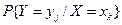 та з’ясувати, чи залежні
та з’ясувати, чи залежні 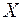 та
та 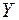 .
.
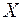
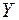
| |||
| -4 | 0.4 | 0.05 | 0.1 |
| -1 | 0.05 | 0.2 | 0.2 |
3. Побудувати функцію регресії 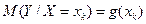 . Знайти рівняння лінійної регресії
. Знайти рівняння лінійної регресії 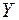 на
на 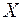 та порівняти її на графику з функцією регресії
та порівняти її на графику з функцією регресії
Розв’язання.1. а) На підставі формули (1) одержимо розподіли координат 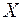 та
та 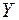 .
.
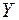
| -4 | -1 |

| 0.55 | 0.45 |
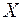
| |||

| 0.45 | 0.25 | 0.3 |
б) 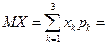 0
0  0.45+2
0.45+2  0.25+4
0.25+4  0.3=1.7;
0.3=1.7;
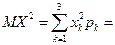 4
4  0.25+16
0.25+16  0.3=5.8;
0.3=5.8; 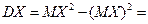 5.8-2.89=2.91;
5.8-2.89=2.91;
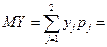 -4
-4  0.55-1
0.55-1  0.45=-2.65;
0.45=-2.65; 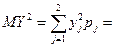 (-4
(-4 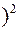
 0.55+(-1
0.55+(-1 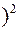
 0.45=8.8+0.45=9.25;
0.45=8.8+0.45=9.25;
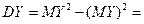 9.25-(2.65
9.25-(2.65 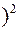 =9.25-7.0225=2.2275.
=9.25-7.0225=2.2275.
в) 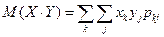 =2
=2  (-4)
(-4)  0.05+4
0.05+4  (-4)
(-4)  0.1+2
0.1+2  (-1)
(-1)  0.2+4
0.2+4  (-1)
(-1)  0.2=-0.4-1.6-0.4-0.8=-3.2. К(Х,У) =М(Х
0.2=-0.4-1.6-0.4-0.8=-3.2. К(Х,У) =М(Х  У)-МХ
У)-МХ  МУ=-3.2-1.7
МУ=-3.2-1.7  (-2.65 ) = -3.2+4.505=1.305.
(-2.65 ) = -3.2+4.505=1.305.
г) 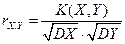 =
= 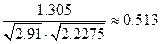 .
.
2. Знайдемо умовні розподіли 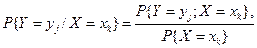 (
( 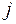 =1,...,
=1,..., 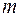 ,
, 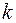 =1,...,
=1,..., 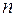 ;
; 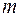 =2,
=2, 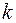 =3), умовні закони розподілу
=3), умовні закони розподілу 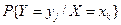 та умовні математичні сподівання
та умовні математичні сподівання 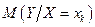 для
для 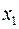 =0,
=0, 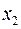 =2,
=2, 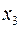 =4.
=4.
а) 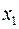 =0. Оскільки
=0. Оскільки 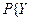 =-4/
=-4/ 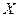 =0}
=0} 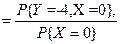 =
= 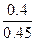 =
= 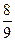 , а
, а
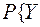 =-1/
=-1/ 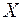 =0}=
=0}= 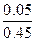 =
= 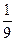 , то умовний закон розподілу
, то умовний закон розподілу 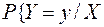 =0}:
=0}:
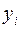
| -4 | -1 |
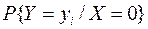
| 8/9 | 1/9 |
,а умовне математичне сподівання  =- 4
=- 4 
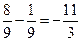
б) 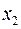 =2. Оскільки
=2. Оскільки 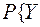 =-4/
=-4/ 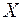 =2}=
=2}= 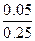 =
=  , а
, а 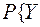 =-1/
=-1/ 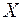 =2}=
=2}=  =
=  , то умовний закон розподілу
, то умовний закон розподілу 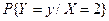 :
:
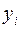
| -4 | -1 |
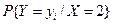
| 1/5 | 4/5 |
,а умовне математичне сподівання
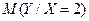 =-4
=-4 
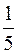 -1
-1 
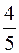 =-
=- 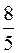 .
.
в) 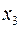 =4. Оскільки
=4. Оскільки 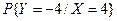 =
= 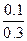 =
= 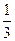 , а
, а 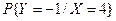 =
= 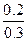 =
= 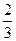 , то умовний закон розподілу
, то умовний закон розподілу 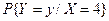 : а умовне математичне сподівання
: а умовне математичне сподівання
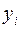
| -4 | -1 |
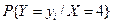
| 1/3 | 2/3 |
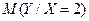 =-4
=-4 
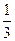 -1
-1 
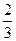 =-2.
=-2.
Оскільки, наприклад, 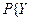 =-4/Х=0}=
=-4/Х=0}= 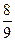
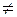
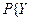 =-4}=0.55, то випадкові величини Х та У - залежні.
=-4}=0.55, то випадкові величини Х та У - залежні.
3. Функція регресії, тобто залежність умовного математичного сподівання 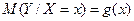 від
від 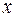 задається таблицею:
задається таблицею:
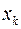
| |||

| -11/3 | -8/5 | -2 |
Рівняння прямої регресії У на Х має вигляд 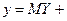 +
+ 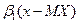 , де
, де 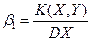 =
= 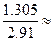 0.45, aбо у=-2.65+0.45(х-1.7), aбо у=-3.415+0.45х. (*) Пряма регресії проходить через точку (МХ;МУ)=(1.7;-2.65). Другу точку на прямій одержимо, поклавши в рівнянні (*) х=0. Тоді друга точка: (0;-3.415). На рис.4 зображені функція регресії
0.45, aбо у=-2.65+0.45(х-1.7), aбо у=-3.415+0.45х. (*) Пряма регресії проходить через точку (МХ;МУ)=(1.7;-2.65). Другу точку на прямій одержимо, поклавши в рівнянні (*) х=0. Тоді друга точка: (0;-3.415). На рис.4 зображені функція регресії 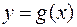 та пряма регресії.
та пряма регресії.
.. 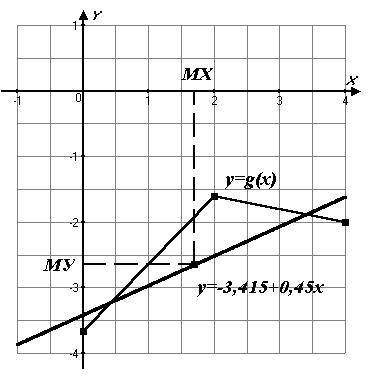
Рис.4
Дата добавления: 2016-10-17; просмотров: 1467;
