Властивості власних значень та власних функцій задачі Штурма-Ліувилля.

1) Крайова задача Штурма-Ліувилля має лічену множину власних чисел, і всі вони є дійсні: .

2) Власні функції, які відповідають різним власним значенням, є ортогональними:

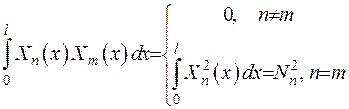
3) Якщо деяка функція 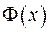має неперервну похідну та кусково-неперервну другу похідну для 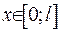, а також задовольняє граничними умовами з (2.6), то її можна розвинути у ряд Фур’є рівномірний та абсолютно збіжний – за власними функціями крайової задачі Штурма-Ліувилля :

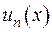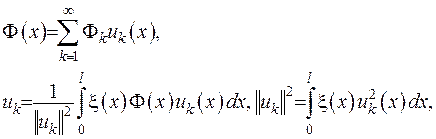
де 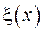- це вага, з якою ортогональні власні функції на проміжку .

Ця властивість крайової задачі Штурма-Ліувилля була сформульована та доведена В.Г.Стекловим і носить назву теореми Стеклова.

Будь-яку функцію, яка задовольняє граничні умови крайової задачі Штурма-Ліувилля, можна розвинути за теоремою Стеклова у рівномірно збіжній ряд за власними функціями, а це означає, що ряд (2.10) є рівномірно збіжний.

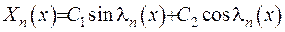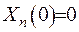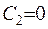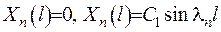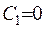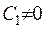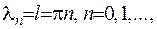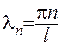Відшукаємо розв’язок задачі Штурма-Ліувилля (2.6). Загальний розв’язок рівняння з (2.6) має вигляд . Задовільним граничну умову , звідки здобудемо . Задовільним граничну умову . Якщо взяти , то отримаємо тривіальний розв’язок рівняння, тому будемо вважати, що . Звідки отримаємо, що тобто - власні числа задачі (2.6), а 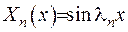- власні функції.

З урахуванням цих властивостей значень та функцій задачі Штурма-Ліувилля (2.6), як один з розв’язків можна брати такий

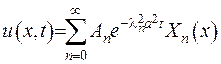(2.7)

Кожен з членів ряду (2.7) задовольняє диференціальне рівняння та крайові умови. Невиконаними залишилися початкові умови. Зробивши перехід до 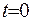, отримаємо

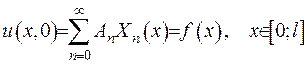. (2.8)

Враховуючи властивість власних значень та власних функцій задачі Ш.-Л. 3), помножимо обидві частини рівності (2.8) на власну функцію 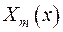та проінтегруємо на проміжку [0;1]

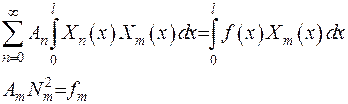(2.9)

звідки отримаємо 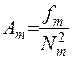. Підставимо значення коефіцієнтів до розв’язку (2.8):

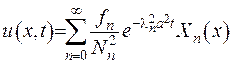, де 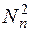- квадрат норми власних функцій. (2.10)

Підрахуємо норму власних функцій:

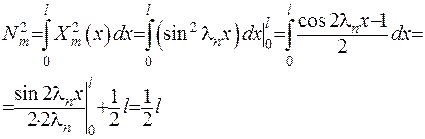
Розв’язок вихідної початково-крайової задачі (2.1) отримано остаточно.

Другий метод розв’язання задач математичної фізики – це метод інтегральних перетворень, суть якого наведено у наступному розділі.