Загальна схема метода.

Розглянемо крайову задачу

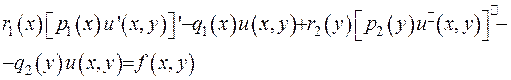(2.11)

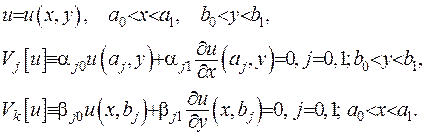
Тут 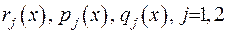- задані функції, 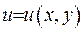- функція, неперервна разом зі своїми похідними.

Будемо розв’язувати задачу (2.11) методом інтегральних перетворень, загальна ідея якого полягає у наступному: розшукується не сама вихідна функція, а інтеграл від неї, що будемо називати трансформантою вихідної функції або інтегральним перетворенням: 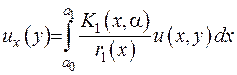. Домножимо обидві частини рівняння з (2.11) на множник та послідовно проінтегруємо всі доданки рівняння.

Розглянемо перший доданок:

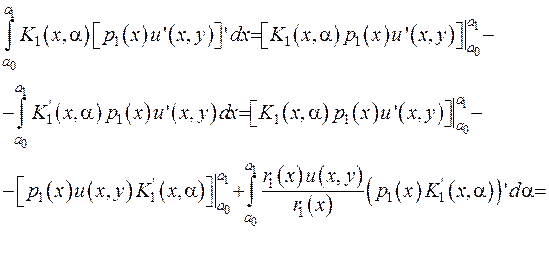
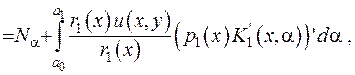
де .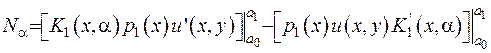

Розглянемо другий доданок; його вигляд після інтегрування:

.

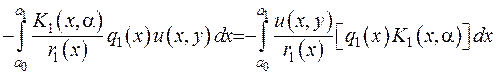Разом перший та другий доданок складають вираз

.

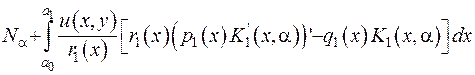Проінтегруємо третій доданок у рівнянні (2.11):

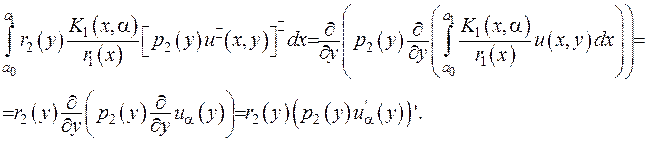Проінтегруємо четвертий доданок рівняння

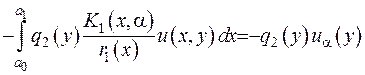
та праву частину .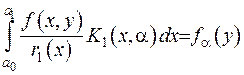

Таким чином, після інтегрування рівняння з (2.11) прийме вигляд

(2.12)

Будемо вимагати, щоб невідома доки що функція 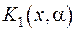задовольняла диференціальне рівняння

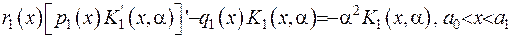(2.13)

Якщо такий розв’язок буде розшукано, то рівняння (2.12) буде зформульовано відносно однієї невідомої функції трансформанти 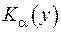. Розглянемо коефіцієнт , після спрощення він набуває вигляду

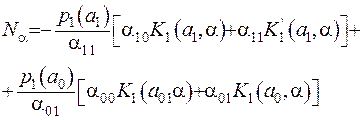(2.14)

Вирази у квадратних дужках можна трактувати як крайові функціонали для ядра перетворення 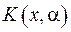. Тоді з цього випливає наступна задача Штурма-Ліувилля для функції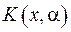

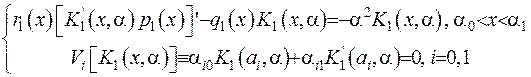(2.15)

Якщо задачу Штурма-Ліувилля (2.15) розв’язати, то рівняння з (2.12) прийме вигляд:

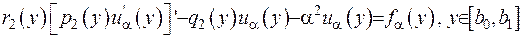(2.16)

Граничні умови перетворюються на вирази:

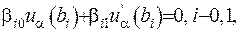або у краткому запису

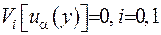(2.17)

Якщо розшукано трансформанту 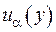, то за нею маємо відновити вихідну функцію.