Постановка крайової задачі Штурма-Ліувілля.

МЕТОДИ РОЗВ’ЯЗАННЯ ГРАНИЧНИХ ЗАДАЧ

МАТЕМАТИЧНОЇ ФІЗИКИ.

Метод відокремлення змінних (метод Фур’є).

Загальна схема метода Фур’є (на прикладі початково-крайової задачі теплопровідності).

Нехай сформульовано наступну задачу теплопровідності:

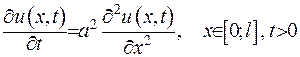(2.1)

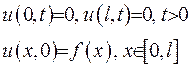
Потрібно побудувати розв’язок початково-крайової задачі (2.1).

Будемо припускати, що невідома функція 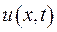дозволяє зображення у вигляді:

. (2.2)

Підставимо зображення (2.2) до рівняння з (2.1):

Поділимо обидві частини отриманої рівності на 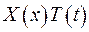. Рівняння набуває вигляду:

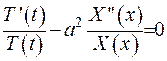
Як бачимо, 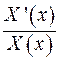має співпадати з деякою сталою, наприклад,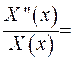

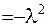. Зробивши таку заміну в (2.3), отримаємо два звичайних диференційних рівняння:

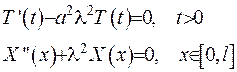(2.4)

Крайові умови з (2.1) після врахування зображення (2.2) запишемо у формі

(2.5)

Додамо крайові умови (2.5) до рівнянь (2.4), та для невідомої функції 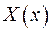отримаємо крайову задачу Штурма- Ліувилля:

(2.6)

Як бачимо, розв’язання задач математичної фізики привело (її розв’язок буде наведено пізніше) до розв’язання задачі Штурма-Ліувілля. Отже розглянемо загальну постанову цієї задачі та її основні властивості.

Постановка крайової задачі Штурма-Ліувілля.

Неважко впевнитися, що крайова задача (2.6) завжди має тривіальний розв’язок. Задача побудови нетривіального розв’язку рівняння з (2.6), що задовольняє граничні умови з (2.6), має назву крайової задачі Штурма-Ліувилля: значення параметру , для яких існує ненульовий розв’язок , називають власними числами задачі (2.6), або власними значеннями, а розв’язки 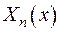, що відповідають кожному власному числу – власними функціями задачі Штурма-Ліувилля.

Розв’язати задачу Штурма-Ліувилля - це означає відшукати всі її власні значення та всі її власні функції.