Інтеграл Фур’є, повне перетворення Фур’є, та - перетворення Фур’є.

Розглянемо часткови випадки:

1)

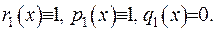
У граничних умовах будемо вважати 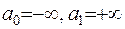. Замість диференціального рівняння з (2.15) запишемо наступне рівняння:

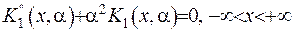(2.18)

загальний розв’язок якого є

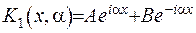(2.19)

За ядро перетворення можна взяти як перший, так і другий доданок. Якщо ядро вибрати у вигляді 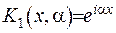, то для трансформанти шуканої функції отримаємо:

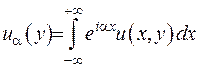(2.20)

Формула (2.20) є інтегральним перетворенням Фур’є.

2) Розглянемо другий частковий випадок, а саме:

.

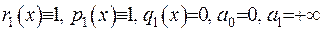Диференційне рівняння (2.18) залишається справедливим на інтервалі , а гранична умова набуває вигляду:

(2.21)

Загальний розв’язок рівняння у цьому випадку запишемо у формі

.

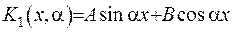Задовільнівши крайову умову (2.21), отримаємо, що стала 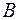дорівнює нулеві. За ядро перетворення візьмемо 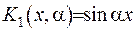. Це приводить до формули інтегрального - перетворення Фур’є 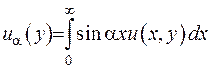. (2.22)

3) Розглянемо ще один частковий випадок, який відрізняється від попереднього тим, що на початку інтервала 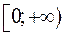задана похідна 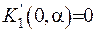. Задовольнимо крайову умову, та отримаємо за описаною вище схемою ядро перетворення .

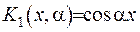Таким чином, запишемо формулу інтегрального 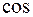- перетворення Фур’є

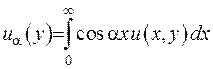. (2.23)

Тепер потрібно отримати формули обернення для інтегрального перетворення Фур’є.

З цією метою потрібно розв’язати інтегральне рівняння

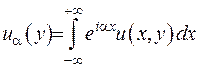, (2.24)

де ліва частина є відомою.

Запишемо поставлену задачу трохи у іншій формі:

.

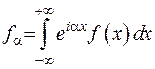Якщо функція 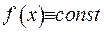, то інтеграл буде розбіжним. Тому потрібна вимога, що 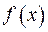є спадною функцією на нескінченності, тобто потрібна абсолютна збіжність такого інтеграла .

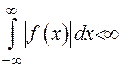Спершу будемо припускати, що функція 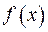задана на скінченому інтервалі 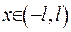та задовольняє умові Діріхле. Тоді використаємо той факт, що її можна розвинути у ряд Фур’є:

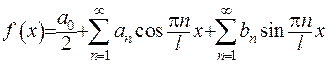, (2.25)

де

.

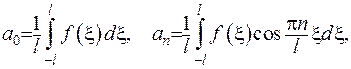
Підставимо коефіцієнти до рівності (2.25)

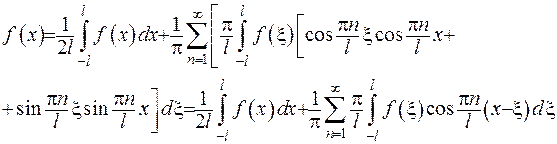(2.26)

Другий доданок у формулі (2.26) є зображенням інтегральної суми для функції 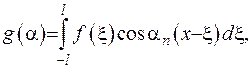, де .

Розглянемо інтеграл

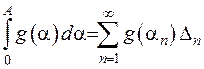. (2.27)

Рівність (2.27) випливає з відомого з аналізу визначення інтеграла через інтегральну суму. Згідно до визначення функції 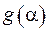можна прийняти за , а за . Тоді з (2.27) випливає

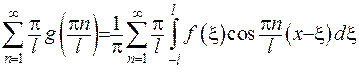
Дійсно, якщо , то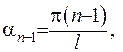

.

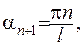
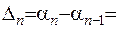
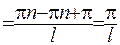Спрямуємо до нескінченності:

.

Перший доданок у формулі (2.26) дорівнюватиме нулеві. Як результат, отримаємо

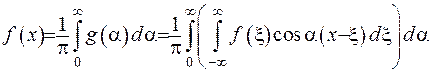(2.28)

Враховуючи співвідношення Ейлера

,

запишемо співвідношення (2.28) у вигляді

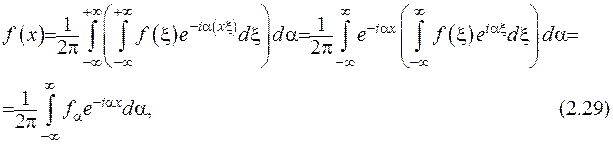
де 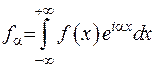- транформанта Фур’є перетворення. Отримана формула (2.29) є формулою оберненого інтегрального Фур’є перетворення. Ця остаточна формула виведена за формальною процедурою (під час виведення застосовано поняття інтегральної суми для півнескінченного інтервала).

Розглянемо важливі часткові випадки інтегрального перетворення Фур’є.

Нехай функція 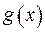задовольняє умові Діріхле та задана на інтервалі 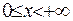. Її трансформанта визначається за формулою

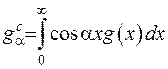(2.30)

Відшукаємо по цій трансформанті вихідну функцію.

Введемо нову функцію 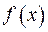, що є парним продовженням функції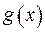

тобто .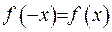

Відповідно до отриманого вище загального перетворення Фур’є

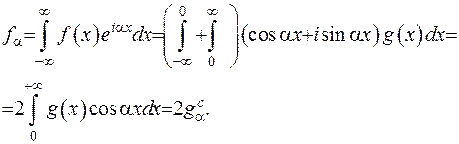
Інтеграл завдяки непарності підінтегральної функції.

Формулу обернення для 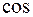-перетворенняФур’є (2.29) запишемо у вигляді:

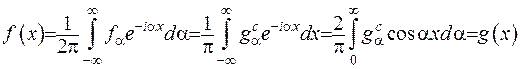(2.31)

Тут використано той факт, що 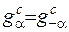. Потрібно відмітити, що вихідну функцію відновлено за умови абсолютної інтегруємості її на дійсній осі - .

Отримаємо тепер формулу обернення для 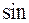- перетворення Фур’є. Для цього продовжимо функцію на проміжок 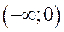непарним чином. Тобто, отримаємо непарну функцію :

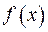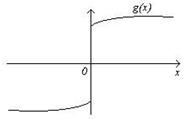
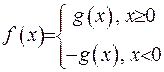
У даному випадку

.

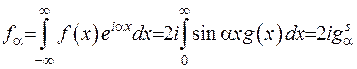Враховуючи, що 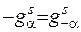, можна записати:

,

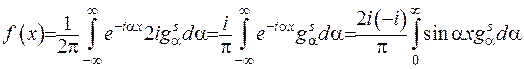тобто маємо

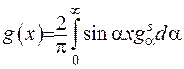(2.32)

формулу оберненого 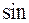- перетворення Фур’є. Щоб цю формулу можна було застосувати, вихідна функція 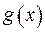мусить бути абсолютно інтегруємо на інтервалі, де вона задана, і для неї мають виконуватися умови Діріхле.