Геометрична інтерпретація задачі лінійного програмування

Задачу лінійного програмування формулюється так. Знайти:

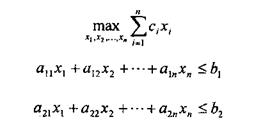
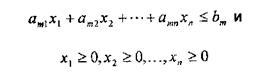
В даному випадку всі умови мають вид нерівностей. Іноді вони можуть бути змішаними, тобто нерівності і рівність:

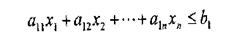
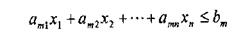
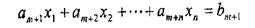
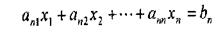
В матричній формі задачу лінійного програмування записують таким чином.

Найти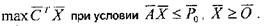

Допустимою безліччю рішень задачі називають будь-яку множину До значень

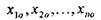задовольняючих приведеним вище умовам лінійного програмування, т.е.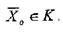

Розглянемо наступний приклад.

ПРИКЛАД 1найти 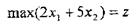за умов

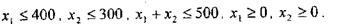
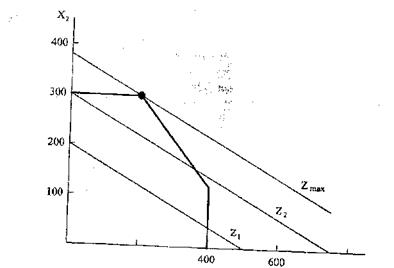
Кожне з цих неравенств-обмежень визначає на півплощини, перетин яких дає багатокутник, який заштрихований на мал.9.6.. Цей багатокутник (опуклий многогранник) і є допустимою безліччю рішень К задачі лінійного програмування

Мал. 9.6. Многогранник рішень в геометричній інтерпретації задач лінійного програмування

Тепер розглянемо цільову функцію, яка має вигляд:

f (x1, x2) = 2x1+5x2_.

Хай f (x1, x2) = 1000 = z.

Графік рівняння 2x₁+5x₂ = 1000 є прямою з відрізками на осях х₁ = 500 одиниць, а х₂ = 200 одиниць.

При f (2x₁+5x₂) = 1500, отримаємо пряму z, що має рівняння:

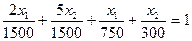
Пряма z паралель прямій z, але розташована вище її. Рухаючи пряму вгору паралельно самої собі, приходимо до такого положення z _mах, коли пряма і множина К, матимуть тільки одну загальну крапку А. Очевидно, що крапка 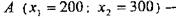оптимальне рішення, оскільки вона лежить на прямій з максимально можливим значенням z.. Помітимо, що ця крапка виявилася крайньою точкою множини К.