Вироджена гіпергеометрична функція.

Вироджена гіпергеометрична функція зображується у вигляді ряда:

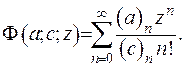(6.48)

Вироджена гіпергеометрична функція задовольняє наступне диференціальне рівняння:

(6.49)

Встановимо область збіжності ряду (6.48). Для цього розглянемо такий випадок гіпергеометричної функції Гауса - 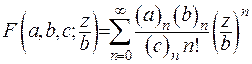. Ряд у правій частині є збіжним при 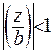або 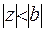. Знайдемо межу :

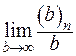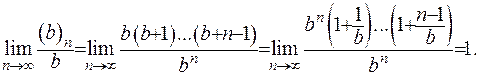
З отриманого випливає, що значення межі гіпергеометричної функції дорівнює

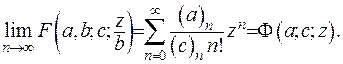
Збіжність гіпергеометричної функції вимагатиме умови 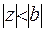, але при прямуванні 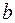до нескінченності, здобудемо, що область збіжності виродженої функції , тобто, ряд є всюди збіжний. Отже, вироджена функція є цілою.

Розглянемо частковий випадок, коли :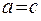

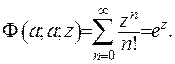
Отримаємо інтегральне зображення виродженої гіпергеометричної функції:

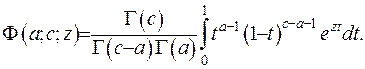(6.50)

Для збіжності цього невласного інтеграла необхідно, щоби виконувалися умови 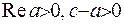(перша умова забезпечує регулярність у нулі, а друга – у одиниці).

Неважко помітити, що, якби множник був би відсутній під інтегралом, то формула (6.50) визначала бета-функцію

(6.51)

Розвинемо множник 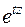у ряд Макгорена, який є рівномірно збіжним, та проведемо почленне інтегрування:

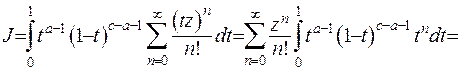
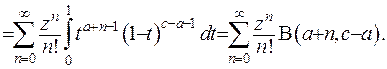(6.52)

Використаємо зображення бета-функції через гама-функцію Гауса (6.13):

(6.53)

Врахуємо тепер, що та сформуємо символ Похгаммера під знаком суми у вираз (6.53):

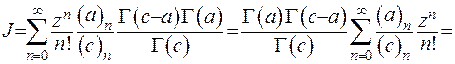
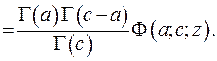(6.54)

Таким чином, доведено формулу інтегрального зображення виродженої гіпергеометричної функції.

Для того, щоб записати формулу диференціювання виродженої гіпергеометричної функції, використаємо вже доведену формулу диференціювання гіпергеометричної функції Гауса:

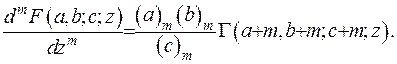
Тоді для виродженої функції маємо

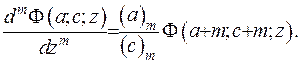(6.55)