Гіпергеометрична функція Гауса.

За означенням гіпергеометрична функція зображується за формулою

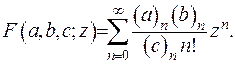(6.21)

Тут 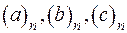- символи Похгаммера. Постійні 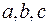та змінна 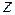, взагалі кажучи, можуть бути комплекснозначними. Що гіпергеометрична функція задовольняє рівняння:

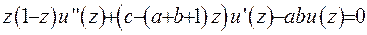(6.22)

Часткове значення функції при 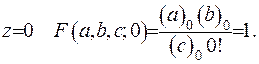З’ясуємо умови, за якими ряд (6.21) збігається. Для цього використаємо принцип Даламбера:

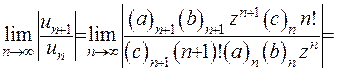
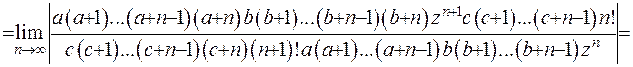
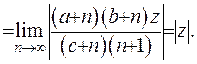(6.23)

Як бачимо, при 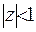ряд (6.21) збігається, при 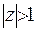розбігається. Якщо 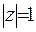, потрібно провести додаткові дослідження, щоб з’ясувати збіжність цього ряду.

Відмітимо певні окремі випадки гіпергеометричної функції. Наприклад, 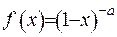. Для цього покажемо, що ця функція є окремим випадком гіпергеометричної функції. Розвинемо цю функцію у ряд Маклорена. Відшукаємо її похідні:

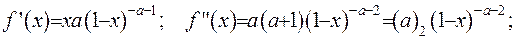
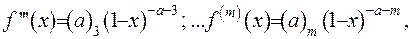
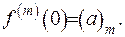
Розвинення у ряд Маклорена набуде вигляду

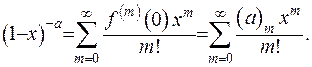(6.24)

Легко бачити, що вираз у (6.24) є частковим випадком гіпергеометричної функції:

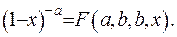
Отримаємо інтегральне зображення функції Гауса. Має місце наступне співвідношення:

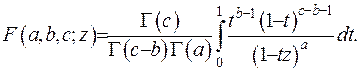(6.25)

Невласний інтеграл (6.25) буде існувати, якщо 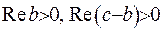. Доведемо зображення (6.25). З цією метою розвинемо вираз 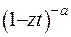у ряд:

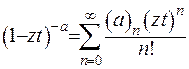
та підставимо його у праву частину рівності (6.25):

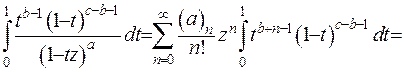
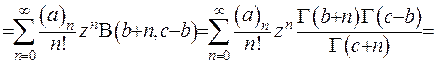
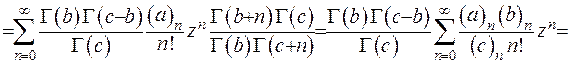
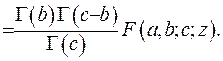(6.26)

Під час отримання співвідношення (6.26) використано той факт, що 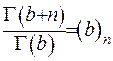. Підставляючи вираз (6.26) у праву частину зображення (6.25), отримаємо тотожність. Отже, інтегральне зображення гіпергеометричної функції доведено.

Ряд, що стоїть у зображенні гіпергеометричної функції, збігається рівномірно за умови 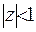, отже можна його диференціювати скільки завгодно разів. Знайдемо першу похідну гіпергеометричної функції:

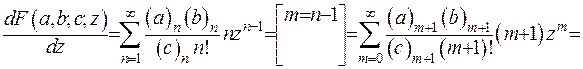
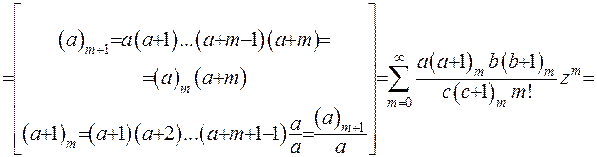
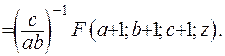(6.27)

Знайдемо за аналогічною схемою другу похідну гіпергеометричної функції:

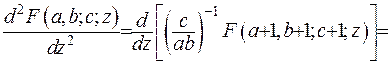
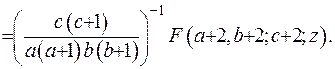
Якщо узагальнити ці результати, то можна записати формулу для відшукування похідної 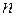-го порядку:

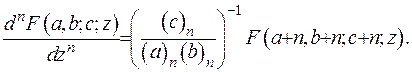(6.28)

Функція Лежандра.

Функції Лежандра є розв’язками наступного диференціального рівняння:

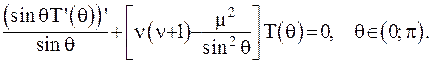(6.29)

Рівняння (6.29) є рівнянням Лежандра.

Проведемо більш детальне дослідження цих важливих для практичних застосувань функцій.

Розглянемо рівняння Лапласа 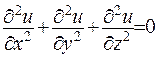, де зробимо перехід до сферичної системи координат 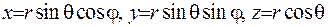. У нових змінних вихідна функція прийме вигляд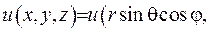

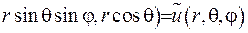. Отже, запишемо рівняння Лапласа у сферичних координатах, враховуючи формулу складної похідної та зв’язок між декартовою та сферичною системами:

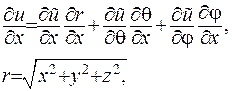
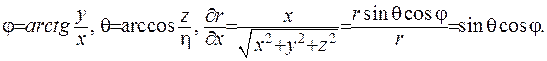
Відшукавши другі похідні за аналогічною схемою, наприкінці отримаємо рівняння Лапласа у сферичних координатах:

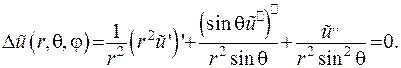(6.30)

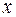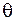Тут штрих позначає похідну за змінною , “ ”– за змінною , а “ “ ” - за змінною .

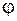Розв’яжемо рівняння (6.30) методом відокремлення змінних, для чого зобразимо шукану функцію наступним чином:

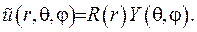(6.31)

Підставимо зображення (6.31) до рівняння (6.30):

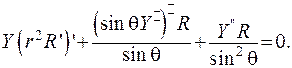(6.32)

Поділимо обидві частини рівності на вираз :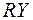

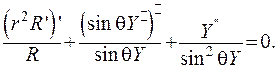(6.33)

Як випливає з методу відокремлення змінних, розв’яжемо два диференціальних рівняння:

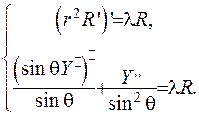(6.34)

Для відшукання функції 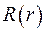отримано рівняння Ейлера:

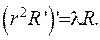
Система (6.33) містить одне звичайне диференціальне рівняння та рівняння у часткових похідних, яке також розв’яжемо методом відокремлення змінних. З цією метою зобразимо функцію 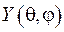у вигляді

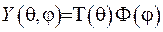. (6.35)

Зображення (6.35) у свою чергу підставимо до другого рівняння системи (6.34):

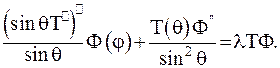(6.36)

Поділимо обидві частини рівності (6.35) на вираз :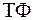

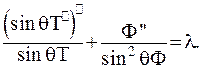(6.37)

Будемо вимагати, щоби

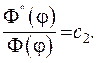(6.38)

Тоді з рівності (6.37) випливає:

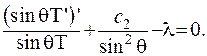(6.39)

Помножимо рівність (6.39) на 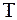, з чого отримаємо диференціальне рівняння для відшукання функції :

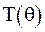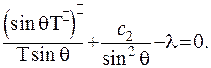(6.40)

Зафіксуємо сталі 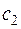та :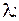

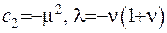Лежандр розглядав випадок 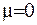. Рівнянню (6.29) задовольняють дві функції – сферичні функції I–го та II-го роду 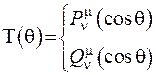(їх іноді називають приєднані функції Лежандра I-го та II-го роду ).

Розглянемо властивості першої з них.

Приєднана функція I-го роду 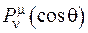може бути зображена через гіпергеометричну функцію:

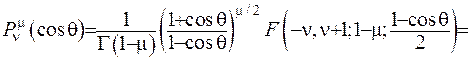
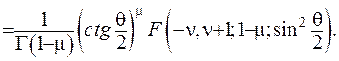(6.41)

Впевнимося, що функція 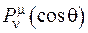дійсно задовольняє рівняння Лежандра. З цією метою зробимо заміну змінних 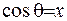, після якої рівняння Лежандра (6.40) прийме алгебраїчний вигляд:

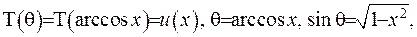
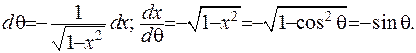
З урахуванням вищенаведених формул маємо:

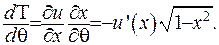
Підставимо значення похідної до першого доданка рівняння (6.40):

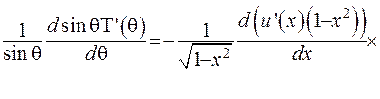
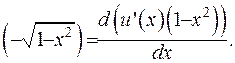(6.42)

У отриманому виразі (6.42) проведемо диференціювання та підставимо отримане значення у рівняння (6.40):

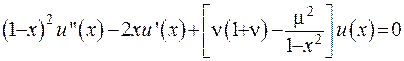. (6.43)

Приєднана функція Лежандра першого роду є розв’язком цього рівняння:

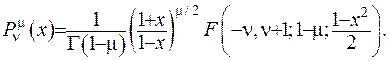(6.44)

Коли 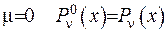- є функція Лежандра , яка виражається через гіпергеометричну функцію

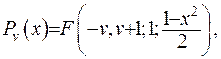або

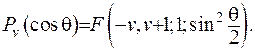(6.45)

Як бачимо, функція Лежандра 1-го роду є регулярною в околі нуля. Якщо вважати 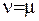- ціле число, то ряд у гіпергеометричній функції обірветься і отримаємо многочлен Лежандра:

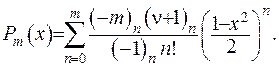(6.46)

Другий розв’язок рівняння Лежандра, сферична функція другого роду

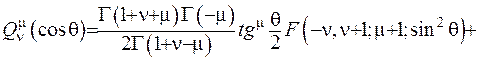
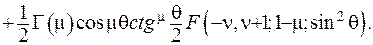(6.47)

На відміну від функції Лежандра 1-го роду, функція 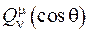у нулі є нерегулярна (бо 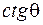у нулі прямує до нескінченності).