Задачі лінійного програмування
В цьому розділі розглянемо приклади задач лінійного програмування.
ПРИКЛАД 13.На двох підприємствах, I і II, ведуться роботи по виробництву двох моделей автомобілів (модель А і модель В). Причому по ряду причин ця робота виконується на кожному підприємстві в течію не більше ніж 30 ч в тиждень. Підприємство I проводить частини для моделі А за 10 ч і частини для моделі В за 5 ч. На підприємстві II збірка моделі А проводиться за 5 ч, а моделі В за 10 ч. Прибуток при продажу моделі А складає 200 фунтів, а моделі В 300 фунтів. Скільки моделей кожного типу {х і у) слід проводити кожного тижня для отримання максимального доходу?
| Підприємство I | Підприємство II | Прибуток | Число | |
| Модель А | х | |||
| Модель В | у |
Перш за все, давайте ясно запишемо всю наявну інформацію. Краще (і для задач лінійного програмування це вже стало традиційним) представляти початкові дані в табличній формі (табл. 9.4.).
Таблиця 9.4
Загальний прибуток 200х + З00у
Оскільки підприємство I працює не більше 30 ч в тиждень, то
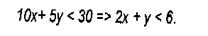
Оскільки підприємство 11 працює не більше 30 ч в тиждень, то
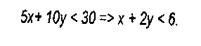
Оскільки продукція не може виражатися негативним числом, то
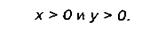
Таким чином, безліч всіх можливих варіантів числа виробів (х, у) може бути представлений у вигляді наступної багатокутної множини (х і у— натуральні числа):
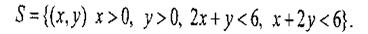
Графічна інтерпретація множини S представлена на мал. 9.15
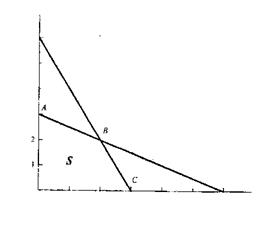
Рис.9.15 Графічна інтерпретація безлічі допустимих значень
задачі прикладу 19.
Координати вершин А, В і З рівні 0 і З,2 і 2,З і 0 відповідно. В одній з цих крапок вираз 200х + З00у приймає найбільше значення. Підстановка значень координат крапок А, В і З в цей вираз показує, що цією крапкою є крапка В. Таким чином, найбільш вигідно проводити кожного тижня дві машини моделі А і дві машини моделі б.
Приведений вище приклад штучний. Змініть його умову так, щоб він більше відповідав дійсності.
ПРИКЛАД 14.З дерева і листового заліза виготовляються іграшки двох типів, партіями по 100 штук кожного типу. На іграшку потрібні наступні матеріали, представлені в табл. 9.5.
Таблиця 9.5
Кількість матеріалів, необхідних для виробництва іграшок

|
На складі є 150 куб. м деревини і 70 кг металу, прибуток від продажу іграшки I типу складає 20 коп., а II типу — 30коп. Яке число партій іграшок кожного типу повинне виготовлятися для отримання максимального прибутку?
ПРИКЛАД 15. На фабриці проводяться звичайна і поліпшена моделі одного і того ж виробу. Для виробництва кожної моделі устаткування використовується відповідно до даних, представлених в табл. 9.6.
Таблиця 9.б
Витрати часу на виробництво виробів

|
Машини працюють не більше 12 ч в доба. Прибуток від звичайної моделі складає 3 крб. і від поліпшеної моделі — 6 крб. Скільки вимагається проводити кожній моделі для отримання максимального прибутку?
ПРИКЛАД 16. Агротехнічний експеримент вимагає, щоб на деяку ділянку було внесено принаймні 30 фунтів фосфатних і 8 фунтів азотних добрив. В лабораторії залишилися від колишніх дослідів 10-фунтові мішки добрив від постачальників А і В. Мінімальна кількість необхідних хімікатів від цих постачальників приведена в табл. 9.7.
Таблиця 9.7
Витрати хімікатів на агротехнічний експеримент

Добрива змішані з піском, який нейтральний, але дає можливість рівномірно розподілити добрива. Разом з тим повинне бути гарантовано дотримання норм внесення добрив. Скільки мішків від кожного постачальника повинне бути узято для виконання вказаних вище вимог. Буде яка загальна вага мішків, доставлених на ділянку?
1.
Дата добавления: 2016-06-13; просмотров: 686;
