Загальна постановка задачі лінійного програмування
більшість задач, вирішуваних методами дослідження операцій, може бути сформульований так.
Вимагається знайти
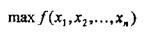
при обмеженнях вигляду
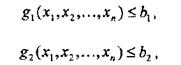
........
gm (x1,x2..., ХП) ≤ bm
— цільова функція або ефективність системи (наприклад, дохід від виробництва якихось виробів, вартість перевезень і ін.); х1,х2...,хп — варіруемі параметри;
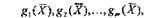 — функції, які задають обмеження на наявні ресурси.
— функції, які задають обмеження на наявні ресурси.
Серед відомих розділів математичного програмування самим розвинутим і закінченим є лінійне програмування (ЛП). Не дивлячись на вимогу лінійності цільової функції і обмежень, в рамки лінійного програмування укладаються багато задач розподілу ресурсів, управління запасами, мережного і календарного планування, транспортні задачі, задачі теорії розкладів і т.д.
Наведемо як приклад досить поширену задачу розподілу літаків по авіалініях.
— кількість літаків j-го типу. Загальне число літаків складає:
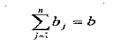
Виходячи з собівартості пасажиро-кілометра і комерційного завантаження кожного типу літака на кожній авіалінії, встановлюють:
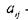 — місячний об'єм перевезень j-м типом літака на i-й авіалінії;
— місячний об'єм перевезень j-м типом літака на i-й авіалінії;
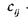 — місячні витрати на експлуатацію j-го типу літака на j-й авіалінії;
— місячні витрати на експлуатацію j-го типу літака на j-й авіалінії;
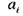 — план перевезень пасажирів по i-й авіалінії.
— план перевезень пасажирів по i-й авіалінії.
Задача полягає в розподілі літакового парку по т авіалініях для перевезення заданої кількості пасажирів при мінімальних витратах.
Позначимо через хij — кількість літаків j -го типу на -й авіалінії.
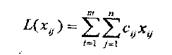
|
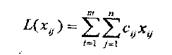
|
Тоді сумарні місячні витрати на експлуатацію
| за умов: |
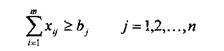
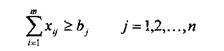
Перша умова означає, що план перевезень повинен бути виконаний, а останнє — обмеження загальної кількості літаків кожного типу.
Потрібен вибрати такі значення хij ≥ 0 (i= 1,2..., m; j = 1,2...,п), які забезпечують мінімум L (хij) при виконанні обох умов.
Дана задача є задачею лінійного програмування.
Дата добавления: 2016-06-13; просмотров: 979;
