Ухвалення рішень в умовах невизначеності
Одним з визначальних чинників в таких задачах є зовнішнє середовище або природа, яка може знаходитися в одному із станів S],S2,...,Sk які невідомі особі, що ухвалює рішення (спостерігач).
Тоді математичну модель задачі в умовах невизначеності можна сформулювати таким чином.
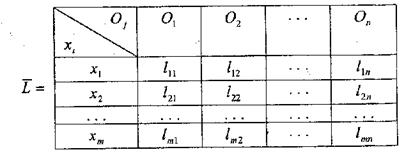
Є деяка матриця L розмірністю т x п, представлена на мал. 9.3.
|
| Мал. 9.3. Матриця ухвалення рішень в умовах невизначеності |
Елемент цієї матриці lij можна розглядати як корисність результату Oj при використовуванні стратегії хi:
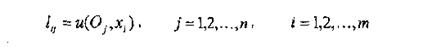
Залежно від стану середи результат 0j досягається з ймовірністю 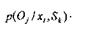
Крім того, спостерігачу невідомо розподіл вірогідності р(Sк). Щодо стану середовища спостерігач може виказувати певні гіпотези. Його припущення про вірогідний стан середовища називаються суб'єктивною вірогідністю р(Sк), к=1,2.,К.
Якби величина р(Sк). була відома спостерігачу, то ми б мали задачу ухвалення рішень в умовах ризику. В цьому випадку вирішальне правило Х1 визначається таким чином:
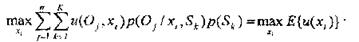
Як вибрати оптимальну стратегію при цьому?
Існує декілька критеріїв для вибору оптимальної стратегії.
1. Критерій Вальда {критерій обережного спостерігача). Цей критерій оптимізує корисність в припущенні, що середовище знаходиться в самому невигідному для спостерігача стані. По даному критерію вирішальне правило має наступний вигляд:
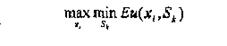
де
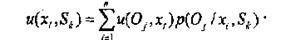
По критерію Вальда вибирають стратегію, яка дає гарантований виграш при якнайгіршому варіанті стану середовища.
2. Критерій Гурвіцазаснований на наступних двох припущеннях:
середовище може знаходитися в самому невигідному стані з вірогідністю
1 — а і в найвигіднішому — з вірогідністю б, де б — коефіцієнт довір'я.
Тоді вирішальне правило записується так:
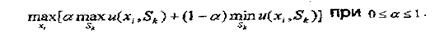
Якщо а = 0, одержуємо критерій Вальда.
Якщо а =1, то приходимо до вирішального правила вида 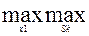
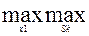 (Xi,Sk), так званої стратегії «здорового оптиміста», який вірить в успіх.
(Xi,Sk), так званої стратегії «здорового оптиміста», який вірить в успіх.
3. Критерій Лапласа. Якщо невідомі стани середовища, то всі стани середовища вважають рівно ймовірними:
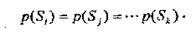
В результаті вирішальне правило визначається співвідношенням:

4. Критерій Севіджа (критерій мінімізації «жалів»). «Жаль» — це величина, рівна зміні корисності результату при даному стані середовища щодо якнайкращого можливого стану.
Щоб визначити «жаль», поступають таким чином.
Його віднімають зі всіх елементів цього стовпця. Далі будуємо матрицю «жалів»
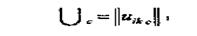
Шукану стратегію X, яка мінімізує «жаль», визначають з умови 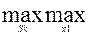 u ikc.
u ikc.
Цей критерій мінімізує можливі втрати за умови, що стан середовища якнайгіршим чином відрізняється від передбачуваного.
Розглянемо окремий випадок запропонованої вище моделі задачі в умовах невизначеності.
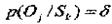
|
Припустимо, що кожному можливому стану середовища відповідає один можливий результат;
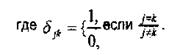
|
Таким чином, в даному випадку математична модель задачі ухвалення рішень визначається безліччю стратегій X = {хі}, безліччю станів середовища S ={Sk}, а також матрицею, яка представлена на рис, 9.4.
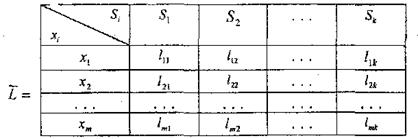
Мал. 9.4.. Матриця відповідності безлічі стратегій безлічі станів середовища
В матриці, представленій на мал. 9, безліч p (Si) передбачається невідомим.
В цьому випадку критерії для вибору оптимальної стратегії мають наступний вигляд:
Критерий Вальда 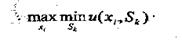
| Критерий Лапласа |
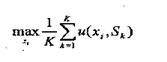
|
Критерий Сэвиджа 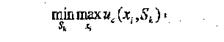
|
Критерий Гурвица 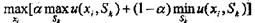
де
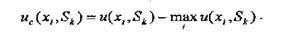
Розглянемо використовування даних критеріїв в умовах невизначеності для практичної ситуації.
ПРИКЛАД 5.Деяка фірма вирішує побудувати готель в одному з курортних місць.
Необхідно визначити найдоцільнішу кількість місць або кімнат в цьому готелі.
Складають кошторис витрат по будівництву готелю з різною кількістю кімнат, а також розраховують очікуваний дохід залежно від кількості кімнат, які будуть зняті.
Залежно від ухваленого рішення — кількості кімнат в готелі х = 20, 30, 40, 50 і кількості знятих кімнат S = 0, 10, 20, 30, 40, 50, яке залежить від безлічі випадкових чинників і невідомо фірмі, одержують таблицю щорічних прибутків (табл. 1).
Таблиця 9.1
Таблиця щорічних прибутків

Найбільш відповідну кількість кімнат в готелі визначають по вищенаведених критеріях.
Критерій Вальда:
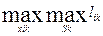 = -121; х опт = 20
= -121; х опт = 20
Судячи з результатів, критерій Вальда не застосовний, оскільки в цьому випадку від споруди готелю слід відмовитися.
Критерій Лапласа:
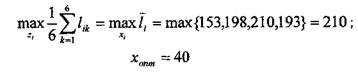
Критерій Гурвіца:
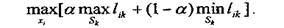
Для різних би можна побудувати таблицю доходів по критерію Гурвіца
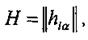
|
Де:
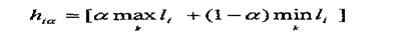
|
Відповідні розрахунки представлені в табл.9.2
Таблиця 9.2
Таблиця доходів по критерію Гурвіца
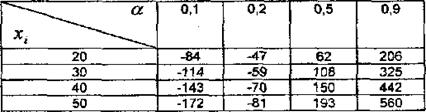
|
Тоді оптимальну кількість кімнат в готелі залежно від α можна представити у вигляді відповідності, яка відображена в табл.3.
Таблиця 9.3
Кількість кімнат в готелі в залежності від а

Критерій Севіджа:
Будуємо матрицю «жалів». Вона відрекомендована на мал. 9.5.
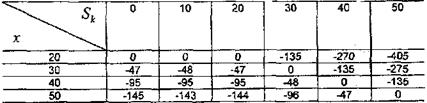
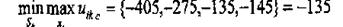
Мал. 9.5. Матриця «жалів» по критерію Севіджа
Таким чином, належить зробити вибір між різними рішеннями:
- по критерію Вальда будувати 20 кімнат;
- по критерію Лапласа будувати 40 кімнат;
- по критерію Гурвіца будувати 20 кімнат, якщо замовник — песиміст і 50 кімнат, якщо він оптиміст;
- нарешті, по критерію Севіджа слід будувати 40 кімнат.
Яке з можливих рішень переважно? Це визначається вибором відповідного критерію (Вальда, Лапласа, Гурвіца або Севіджа).
Вибір критерію ухвалення рішення є найскладнішим і відповідальним етапом в дослідженні операцій. При цьому не існує яких-небудь загальних рекомендацій або порад. Вибір критерію повинен проводити замовник на найвищому рівні і в максимальному ступені погоджувати цей вибір з конкретною специфікою задачі, а також з своєю метою.
Зокрема, якщо навіть мінімальний ризик недопустимий, то слід застосовувати критерій Вальда. Якщо навпаки, певний ризик цілком прийнятний і замовник має намір вкласти в деяке підприємство стільки засобів, щоб потім він не жалкував, що вкладено дуже мало, то вибирають критерій Севіджа.
За відсутності достатньої інформації для вибору того або іншого критерію можливий альтернативний підхід, який пов'язаний з обчисленням шансів на успіх і розорення на основі минулого досвіду.
Дата добавления: 2016-06-13; просмотров: 968;
