Ухвалення рішень в умовах визначеності

Ухвалення рішень в умовах визначеності характеризується однозначним або детермінованим зв'язком між ухваленим рішення і його результат. Основна трудність — наявність декількох критеріїв, по яких слід порівнювати результати.

Тут виникає задача ухвалення рішень при так званому «векторному критерії».

Випадок 1. Хай є сукупність критеріїв:

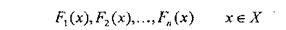
Знайти рішення, яке виявиться якнайкращим в значенні вибираного критерію.

Якщо всі критерії вимірюються в одній шкалі, то узагальнений критерій F0 (х) можна записати у вигляді зваженої суми цих критеріїв

де w_i — вага відповідного критерію. В цьому випадку необхідно знайти max F0 (х).

Якщо ж ці критерії вимірюються в різних шкалах, то необхідно привести їх до однієї шкали. Для цього формують критерій

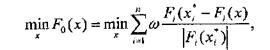
де

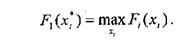
Отже, вимагається звести до мінімуму величину ухилення кожного критерію від його максимального значення.

При такому формуванні узагальненого критерію виникає деяка невідповідність, зв'язана з тим, що можна добитися високих показників по одних критеріях за рахунок погіршення показників по інших. В цьому випадку значення деяких приватних критеріїв можуть виявитися менше гранично допустимих значень:

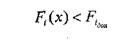
Проте часто необхідно, щоб виконувалася наступна умова:

Тому можна запропонувати ще один спосіб утворення узагальненого критерію.

Припустимо, що по кожному критерію визначені граничні значення F_iдоп, i = .

Якщо умова F_i (х) ≥ F_iдоп виконується, то можна прийняти F_i (х) рівним власному значенню F_i (х) = F_i (х).

Якщо ця умова не виконується, то потрібно прийняти F_i (х) = -∞.

У такому разі задача зводиться до знаходження

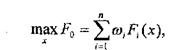
при приведеній умові.

Випадок 2. Припустимо, що критерії впорядковані в послідовності F₁,F_2,…, F_п.

Тоді задача відшукання оптимального рішення може бути записаний як

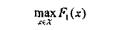
при обмеженнях:

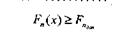
ПРИКЛАД 4. Припустимо, що кому-небудь не обходжений ухвалити рішення про вибір нареченої. Ми тут не розглядаємо варіанти невизначеності майбутнього. Умовно вважаємо, що в даний час наш «герой» володіє повною інформацією про своїх «подружок». І перед ним стоїть задача, з урахуванням своїх переваг, вибрати найбільш відповідну супутницю життя.

Рішення задачі включає декілька кроків (операцій).

1. Визначення безлічі рішень.

Припустимо, що наш «наречений» має п'яти знайомих дівчат і вони згодні вийти за нього заміж: Люду, Таню, Аллу, Олю, Лілю.

2. Визначення значущих чинників.

Далі ми для нього {а може і він сам) визначаємо значущі чинники у виборі кандидатури:

F₁ - добра фігура;

F₂ - красиве обличчя;

F₃ - еротичність;

F₄ - уміння готувати пищу;

F₅ - душевна доброта;

F₆ - веселість характеру.

3. Визначення значення чинників для всіх змінних.

Тепер «наречений», і лише він, визначає значення в числовому виразі кожного чинника для всіх кандидаток в майбутні дружини. Перед цим необхідно умовитися, що значення кожного чинника змінюється в цілих числах від одиниці до, наприклад, двадцяти.

Результати цього дослідження приведені в матриці, представленій на мал. 9.1.

4. Визначення терезів чинників.

Далі, знову таки «наречений» і лише він, визначає вагові категорії кожного чинника. На цьому етапі він відображає свою точку зору на значущість для нього виділених чинників. Помітимо, що, з одного боку, у різних людей можуть бути самі різні переваги, з іншою - з віком ми завжди трансформуємо свою «шкалу цінностей». У будь-якому випадку вагові категорії відображають «бачення проблеми» замовником (в даному випадку - «нареченим»).

Мал. 9.1. Приклад матриці для ухвалення рішення в умовах

визначеності

Хай (вважатимемо, що він достатньо молодий) визначена наступна вага (заздалегідь домовимося, що вага визначається цілими числами в межах від 1 до 10):

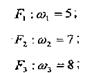
F6 : w6= 3.

5. Визначення значення в умовах визначеності..

Останній крок - це визначення самої відповідної кандидатури. Після того, як побудована формальна модель, проблема розв'язується за допомогою наступної формули:

Наречена =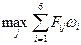

Розрахуємо всі можливі значення: Люда = 125; Таня = 263; Алли = 185; Оля = 242; Ліля = 274. Таким чином, в нашому прикладі «наречена = Ліля».

Розглянутий приклад, звичайно, в значній мірі носить жартівливий характер. Проте, він повністю демонструє єство підходу дослідження операцій при ухваленні рішення в умовах визначеності.