Задачі вибору маршруту

Задачі вибору маршруту, або мережні задачі частіше за все зустрічаються при дослідженні різноманітних процесів на транспорті і в системах зв'язку. Типовою задачею є задача знаходження деякого маршруту проїзду з міста А в місто В за наявності декількох маршрутів для різних проміжних пунктів. Вартість проїзду і затрачуване на проїзд час залежать від вибраного маршруту. Визначити най економічний маршрут по вибраному критерію оптимальності.

На допустимі маршрути може бути накладений ряд обмежень. Так, вводять заборону на повернення до вже пройденого пункту (вузлу сіті) або вимогу обходу всіх пунктів сіті при умові, що в кожному пункті можна побувати тільки один раз (задача комівояжера).

В пунктах сіті можливі затримки (наприклад, на перехрестях шосейних доріг). Ці затримки залежать від навантаження на вузол, зайнятості витікаючих комунікацій, обмеженої пропускної спроможності пунктів сіті або носять випадковий характер.

Серед мережних задач найпоширенішими є задача вибору найкоротшого шляху між довільними пунктами сіті, задача комівояжера, задача про максимальний потік.

На мал. 8.3. представлений умовний приклад графічного трактування задач вибору маршруту. Помітимо, що спеціально «порушена» топологія розміщення населених пунктів. Йдеться про математичну постановку задачі. Тому, відповідна топологія розміщення міст повинна бути відображений в даній задачі.

Комбіновані задачі

Комбіновані задачі включають декілька типових моделей задач одночасно. Наприклад, при плануванні і управлінні виробництвом доводиться вирішувати наступний комплекс задач:

1)скільки виробів кожного типу необхідні випустити і які оптимальні розміри партій виробів? (Типова задача планування виробництва);

2)розподілити виробничі замовлення по видах устаткування після того, як визначений оптимальний план виробництва. (Типова задача розподілу);

3) в якій послідовності і коли слід виконувати виробничі замовлення? (Типова задача календарного планування).

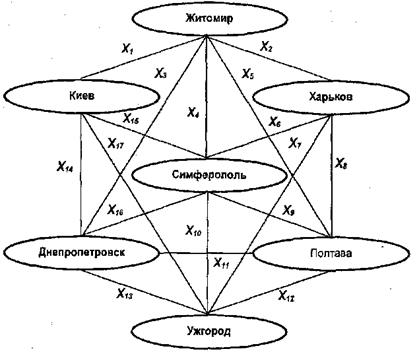
Мал. 8.3. Графічна інтерпретація задачі комівояжера

Оскільки ці три задачі не можна вирішити ізольований, незалежно один від одного, то можливий наступний підхід до рішення даної комбінованої задачі. Спочатку одержують оптимальне рішення задачі планування виробництва. Потім залежно від цього оптимуму знаходять якнайкращий розподіл устаткування. Нарешті, на основі такого розподілу складають оптимальний графік виконання робіт.

Проте така послідовна оптимізація приватних під задач не завжди приводить до оптимального рішення задачі в цілому. Зокрема, наприклад, може виявитися, що не можна провести всі вироби в оптимальних кількостях через обмеженість наявних ресурсів. Поки що не знайдений метод, що дозволяє отримати одночасний оптимум для всіх трьох задач, а можливо він не існує для конкретних задач. Тому для вирішення подібних комбінованих задач застосовується метод послідовних наближень, що дозволяє наблизитися до шуканого рішення комбінованої задачі достатньо близько.

Можливо, рішення таких комбінованих задач повинне бути засновано на застосуванні гібридних систем.

Під гібридними системами розуміються інтегровані комплекси формальних методів (дослідження операцій і математичного моделювання) і евристичних методів (реалізованих у формі експертних систем з базами знань).

Загальна архітектура систем такого класу представлена на мал. 8.4. Замети, що фахівці в області штучного інтелекту такі системи називають гібридними експертними, а фахівці в області математичного моделювання - інтелектуальними пакетами прикладних програм. В даний час на їх основі розробляються системи аналітичної підтримки ухвалення рішень.

Мал. 8.4.. Сучасні комп'ютерні технології систем аналітичної підтримки ухвалення рішень

Запропонована класифікація задач дослідження операцій не є остаточною. З часом деякі класи задач

об'єднуються, і стає можливим їх сумісне рішення, стираються межі між вказаними класами задач, а також з'являються нові класи задач.

Контрольні питання:

1. Охарактеризуйте задачі операційного дослідження?

2. Цілі та зміст задач масового обслуговування?

3. Особливості задач планування та управління?

4. Підходи до використання задач вибору маршруту?

5. Які особливості застосування комбінованих задач?

Лекція 9. ДЕЯКІ ПРИНЦИПИ УХВАЛЕННЯ РІШЕНЬ В ЗАДАЧАХ ДОСЛІДЖЕННЯ ОПЕРАЦІЇ ( 4 год.)

ПЛАН