Задачі ремонту і заміни устаткування

Задачі ремонту і заміни устаткування з'являються в тих випадках, коли працююче устаткування зноситься, застаріває і з часом підлягає заміні.

Зношене устаткування піддають або попереджувально-відновному ремонту, поліпшуючому його технологічні характеристики, або повній заміні. При цьому можлива постановка задачі така. Визначити терміни відновного ремонту і момент заміни устаткування модернізованим, при яких сумарні очікувані витрати по ремонту і заміні, а також втрати унаслідок погіршення технологічних характеристик — старіння за весь час експлуатації устаткування — мінімізуються.

Існує і таке устаткування, в якому деталі повністю виходять з ладу, не відновлюються і підлягають заміні (наприклад, електронні лампи, що перегоріли). Постановка задачі в цьому випадку наступна. Визначити терміни профілактичного контролю по виявленню несправностей, при яких сумарні витрати на проведення контролю і втрати від простою устаткування через невчасне виявлення і заміну що вийшли з ладу деталей мінімізуються.

2. Задачі масового обслуговування, впорядкування, планування і управління

Задачі масового обслуговування розглядають питання освіти і функціонування черг, з якими доводиться стикатися в повсякденній практиці і в побуті. Наприклад, черги літаків, що йдуть на посадку, клієнтів в ательє побутового обслуговування, абонентів, чекаючи виклик на міжміській телефонній станції і т.д.

Черги виникають через те, що потік вимог або клієнтів на обслуговування некерований і випадковий. Якщо кількість приладів обслуговування (злітно-посадочні смуги аеродрому, приймальники в ательє побутового обслуговування, канали зв'язку і т. д.) достатньо велика, то черга утворюється рідко, проте неминучі тривалі простої устаткування. З другого боку, при малій кількості приладів створюється значна черга і будуть великі втрати через очікування в черзі. Тому можлива наступна постановка задач масового обслуговування. Визначити, яка кількість приладів обслуговування необхідна, щоб мінімізувати сумарні очікувані втрати від невчасного обслуговування і простоїв устаткування.

Задачі впорядкування характеризуються наступними особливостями. Наприклад, є безліч різних деталей з певними технологічними маршрутами, а також декілька одиниць устаткування (фрезерний, токарний і стругальній верстати), на яких ці деталі обробляються. Оскільки одночасно обробляти більше однієї деталі на одному верстаті неможливо, у деяких з верстатів може утворитися черга робіт, тобто деталей, що чекають обробки. Час обробки кожної деталі відомо. Визначити таку черговість обробки деталей на кожному верстаті, при якій мінімізується деякий критерій оптимальності, наприклад, сумарна тривалість завершення комплексу робіт. Така задача називається задачею календарного планування або складання розкладу, а вибір черговості запуску деталей в обробку — впорядкуванням.

Критерії оптимальності, що використовуються в задачах календарного планування мають різний вигляд. Найбільш часто зустрічаються наступні критерії:

1. Мінімізація загальної тривалості робіт, тобто інтервалу часу між моментом початку першої операції і моментом закінчення останньою.

2. Мінімізація загального запізнювання. Запізнювання визначається як різниця між фактичним і директивним терміном завершення обробки по кожній деталі. Загальне запізнювання є сумою запізнювань по всіх деталях.

3. Мінімізація максимального запізнювання, тобто мінімізація запізнювання по тій деталі, для якої ця величина є найбільшою.

4. Мінімізація втрат, обумовлених запізнюванням.

Задачі мережного планування і управління (СПУ). В цьому класі задач розглядається співвідношення між терміном закінчення крупного комплексу операцій і моментами початку всіх операцій комплексу. Вони актуальні при розробці складних і дорогих проектів. Для строгої постановки задач необхідні такі умови:

- повинна існувати точно визначувана безліч операцій, які треба виконати для завершення всього комплексу, що включає ці операції як своїх

елементів;

- безліч операцій комплексу впорядкована так, що для кожної операції відомо, які операції безпосередньо їй передують, а які слідують за нею;

- в межах заданого відношення впорядкування операції можна починати і закінчувати незалежно один від одного;

- відомий взаємозв'язок між величиною споживаного ресурсу і тривалістю кожної операції.

Комплекс операцій в цьому випадку можна представити у вигляді мережного графіка, що складається з вершин (вузлів) і орієнтованих дуг. В цьому випадку операцій зображають дугами, а вершини є деякими подіями. Дуги, що входять у вершину, відповідають операціям, які повинні бути закінчений раніше, ніж можна буде почати операції, зображені витікаючи ми дугами. Події, відповідному початку виконання комплексу, привласнюють номер 0.

Решту подій нумерують так, що, якщо події i, j зв'язані деякою операцією ( i- j ), то виконується, нерівність , де —моменти настання подій i, j, а t_ij — тривалість операції (i - j) .

На мал. 8.2 умовний приклад представлено графічною інтерпретацією задач мережного планування і управління.

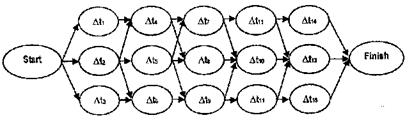
Мал. 8.2.. Графічна інтерпретація задачі мережного планування і управління

Якщо виконуються вищевикладені умови і допущення, можливі наступні постановки задач мережного планування і управління:

1. Задана тривалість всього комплексу. Визначити термін початку кожної операції, при яких мінімізується один з наступних критеріїв:

а) загальні витрати на виконання всього комплексу робіт

б) середньоквадратичний показник нерівномірності споживаних ресурсів;

в) вірогідність невиконання комплексу робіт в директивний термін;

г) середньоквадратичне відхилення необхідних ресурсів від готівки.

2. Задані загальні ресурси. Визначити терміни початку кожної операції, при яких мінімізується тривалість виконання всього комплексу робіт.