Основні етапи операційного дослідження
При всьому різноманітті змісту конкретних робіт по дослідженню операцій кожне операційне дослідження проходить послідовно наступні основні етапи:
1) постановка задачі
2)побудова математичної моделі
3) знаходження методу рішення
4) перевірка і коректування моделі
5) реалізація знайденого рішення на практиці.
Постановка задачі— це надзвичайно відповідальний етап операційного дослідження. Спочатку задачу формулюють з погляду замовника. Така постановка задачі звичайно не буває остаточною. Під час аналізу досліджуваної системи задача поступово уточнюється. На цьому етапі роль операційної групи полягає в проведенні ретельного обстеження об'єкту, вивченні безлічі чинників, що впливають на результати досліджуваного процесу.
Після збору даних обстеження і їх аналізу операційна група виділяє сукупність істотних чинників, проводить консультації із замовниками і уточнює остаточно змістовну (словесну) постановку задачі.
Для з'ясування упущених чинників і їх взаємозв'язків при необхідності проводять додаткове обстеження об'єкту.
Побудова математичної моделі.Отримавши достатньо строгу і логічно несуперечливу, змістовну постановку задачі, потрібно побудувати її математичну модель. Цей процес називається формалізацією задачі.
В найзагальнішому випадку математична модель задачі має
вигляд:
знайти
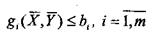
— цільова функція (показник якості або ефективність системи);
 — вектор керованих змінних;
— вектор керованих змінних;
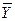 — вектор некерованих змінних;
— вектор некерованих змінних;
gi — функція споживання i-го ресурсу;
bi — величина i-го ресурсу (наприклад, планова фундація машинного часу групи токарних автоматів в станко-годиннику).
Знаходження методу рішення. Для знаходження оптимального рішення  опт задачі (1) залежно від структури цільової функції і обмежень застосовують ті або інші методи теорії оптимальних рішень, звані також методами математичного програмування:
опт задачі (1) залежно від структури цільової функції і обмежень застосовують ті або інші методи теорії оптимальних рішень, звані також методами математичного програмування:
1. Лінійне програмування, якщо f (  ) і gi (
) і gi (  )— лінійні функції щодо змінних
)— лінійні функції щодо змінних  .
.
2. Нелінійне програмування, якщо f (  ) і gi (
) і gi (  ) — нелінійні функції.
) — нелінійні функції.
3.Динамічне програмування, якщо f (  ) має специфічну структуру, тобто є адитивною або мультиплікативною функцією від змінних
) має специфічну структуру, тобто є адитивною або мультиплікативною функцією від змінних  .
.
4.Геометричне програмування, якщо цільова функція, а обмеження  а ообмеження
а ообмеження 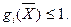
5.Стохастичне програмування, коли 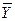 — випадкова величина, а замість функції f (
— випадкова величина, а замість функції f (  ) розглядають її математичне очікування М у [ f (
) розглядають її математичне очікування М у [ f (  )].
)].
6.Дискретне програмування, якщо на змінні  накладена умова дискретності (наприклад, вимога цілочисельності).
накладена умова дискретності (наприклад, вимога цілочисельності).
7.Евристичне програмування застосовують для вирішення тих задач, в яких точний оптимум знайти алгоритмічним шляхом неможливо через величезне число варіантів. У такому разі відмовляються від пошуку оптимального рішення і відшукують достатньо добре (або задовільне з погляду практики) рішення. При цьому користуються спеціальними прийомами — евристиками, дозволяючи ми істотно скоротити число проглядаються варіанти. Евристичні методи також застосовують, коли оптимальне рішення у принципі може бути знайдено (тобто задача алгоритмічно вирішувана), проте для цього потрібні об'єми ресурсів, значно перевищуючі наявні.
З перерахованих вище методів математичного програмування самим розвинутим і закінченим є лінійне програмування. В його рамки укладається широкий круг задач дослідження операцій.
Перевірка і коректування моделі. В складних системах, до яких відносяться системи організаційного типу, модель лише частково відображає реальний процес. Тому необхідна перевірка ступеня відповідності або адекватності моделі і реального процесу. Перевірку проводять порівнянням передбаченої поведінки з фактичним при зміні значень зовнішніх некерованих дій.
Перевірку і коректування моделі можна проводити, наприклад, по логічній схемі, показаній на мал. 8.1., де  — вектор керованих змінних, — вектор некерованих змінних, Х вих.о — вихідні параметри об'єкту,
— вектор керованих змінних, — вектор некерованих змінних, Х вих.о — вихідні параметри об'єкту,
Х вих.м — вихідні параметри моделі.
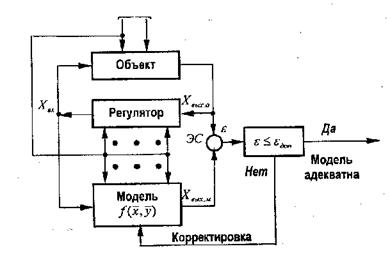
| Мал. 8.1. Логічна схема коректування і перевірки моделі |
Величини Хвих.о і Х вих.м подаються на елемент порівняння (ЕС), і обчислюється величина помилки в  . Якщо величина перевищує допустиме значення відхилення ε доп (його вибирають, виходячи з необхідного ступеня адекватності моделі), то це свідчить про те, що упущені деякі важливі чинники і взаємозв'язки. В цьому випадку модель коректують.
. Якщо величина перевищує допустиме значення відхилення ε доп (його вибирають, виходячи з необхідного ступеня адекватності моделі), то це свідчить про те, що упущені деякі важливі чинники і взаємозв'язки. В цьому випадку модель коректують.
Коректування може зажадати додаткові дослідження об'єкту, уточнення структури математичної моделі, численних змін змінних моделі. Таким чином, чотири названі вище за етап повторюють багато разів до тих пір, поки не буде досягнута задовільна відповідність між виходами об'єкту і моделі.
Реалізація знайденого рішення на практиці є найважливішим етапом, завершальним операційне дослідження. Упровадження можна розглядати як самостійну задачу, застосувавши до неї системний підхід і аналіз. Отримане заздалегідь математичне рішення вдягаються у відповідну змістовну форму і представляють замовнику у вигляді інструкцій і рекомендацій.
З погляду реалізації оптимального рішення на практиці дослідження операцій займає особливе місце в проблематиці інформаційних технологій. Відомо, що упровадження інформаційних технологій ефективно для вирішення таких задач управління, які неможливо вирішити при що склалася раніше практиці управління. Тому в даний час висунуть так званий принцип нових задач АСУ. Під цим принципом розуміється пошук і постановка на виробництві дійсно нових задач оптимального управління, які можуть окупити витрати на створення АСУ. Дослідження операцій і є методологічною основою для знаходження таких задач, розробки їх математичних моделей і алгоритмів рішення, а також для практичного упровадження оптимального рішення.
На виробництві виконують операційне дослідження. На основі матеріалів дослідження проводять системний аналіз об'єкту і визначають задачі управління, які дають найвідчутніший ефект в результаті автоматизації. Виходячи з принципу системного підходу розробляють математичні моделі цих задач і алгоритми рішення. Практична ж реалізація вказаних задач, тобто їх упровадження буде здійснено при створенні відповідних інформаційних технологій.
Дата добавления: 2016-06-13; просмотров: 2507;
