Аксіома неперервності та її еквівалентність аксіомі зліченної адитивності
Аксіомою неперервностіймовірності називають твердження:
Р4. Якщо B1, B2, ... , Bn, ... – монотонно незростаюча послідовність випадкових подій і така, що  , то
, то
 .
.
Теорема 3. Аксіоми зліченної адитивності та неперервності ймовірності еквівалентні.
Доведення. Доведемо, що з аксіоми Р3 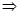 аксіома Р4.
аксіома Р4.
Дійсно, з теореми 5.2, доведення якої базується на аксіомі Р3, випливає
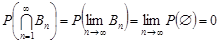 .
.
Доведемо, що з аксіоми Р4 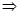 аксіома Р3.
аксіома Р3.
Нехай А1, А2, ... , Аn, ... – послідовність попарно несумісних випадкових подій з 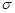 - алгебри F. Покладемо
- алгебри F. Покладемо  . Тоді
. Тоді  , для
, для 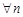 і
і  . Враховуючи виконання властивості скінченої адитивності для попарно несумісних випадкових подій, маємо
. Враховуючи виконання властивості скінченої адитивності для попарно несумісних випадкових подій, маємо
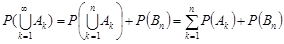 .
.
Оскільки  , то
, то
 =
=  .
.
Теорема доведена.
Висновок. Система аксіом А.М. Колмогорова дозволяє будувати теорію ймовірностей як частину теорії міри, бо ймовірність можна розглядати як невід’ємну нормовану адитивну функцію множини F. Зазначимо також, що введена система аксіом є неповною, бо навіть для одного стохастичного експерименту можна будувати різні ймовірнісні моделі (парадокс Бертрана). Але ця ж сама система аксіом є не суперечною, бо існують реальні об’єкти, які всім цим аксіомам задовольняють. Наприклад, це стосується стохастичних експериментів, які вписуються в класичну схему ймовірностей.
Дата добавления: 2016-11-02; просмотров: 1107;
