Теореми неперервності ймовірності

Для доведення деяких властивостей ймовірності, які були розглянуті в лекції 4, застосовувалась лише аксіома скінченої адитивності. Наведемо теореми, для виконання яких треба використати аксіому зліченної адитивності.

Теорема 5.1. Якщо А₁, А₂, ... , А_n, ... – монотонно неспадна послідовність випадкових подій, тобто

,

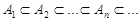то

.

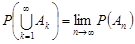Доведення. Оскільки послідовність випадкових подій А₁, А₂, ... , А_n, ... – монотонно неспадна, об’єднання їх можна представити у вигляді об’єднання попарно несумісних подій:

.

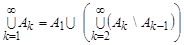До правої частини цієї рівності застосуємо аксіому зліченної адитивності А3. Маємо

.

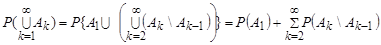Згідно аксіомі Р3 ряд у правій частині цієї рівності збігається. Як відомо, його сума 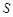дорівнює границі частинній сумі 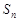при . Знайдемо :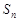

.

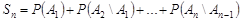Оскільки 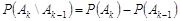, то

.

Звідки 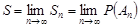. Теорема доведена.

Зауваження. Якщо А₁, А₂, ... , А_n, ... – монотонно неспадна послідовність випадкових подій, то 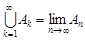. Отже, твердження доведеної теореми можна записати так:

,

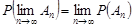тобто можна переходити до границі під знаком імовірності. В силу цього, теорему 5.1 називають властивістю неперервності ймовірності.

Теорема 5.2. Якщо А₁, А₂, ... , А_n, ... – монотонно незростаюча послідовність випадкових подій, тобто

,

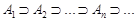то

.

Доведення. За властивістю 2 ймовірності та правилами де Моргана

.

Оскільки А₁, А₂, ... , А_n, ... – монотонно незростаюча послідовність випадкових подій, то послідовність протилежних подій – монотонно неспадна послідовність. Отже, за теоремою 5.1

.

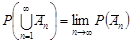Таким чином,

.

Теорема доведена.

Зауваження. Аналогічно зауваженню до теореми 1, твердження теореми 2 можна записати так:

.

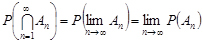Тому теорему 5.2 також називають властивістю неперервностіймовірності.