Геометричне означення ймовірності випадкових подій

Класичне означення ймовірності застосовується лише тоді, коли стохастичний експеримент можна описати простором скінченої кількості рівноможливих елементарних подій. У випадку невиконання цих умов відповідна формула (2.1) не може бути застосована. Узагальнимо поняття класичної ймовірності. Перш за все розглянемо таку задачу: припустимо, що на деякий відрізок прямої 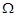навмання ставиться точка. Нехай А 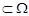. Доречно припустити, що ймовірність попадання точки в проміжок А пропорційна довжині цього проміжку, тобто

,

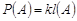де k – коефіцієнт пропорційності, 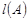– довжина проміжку А. Коефіцієнт пропорційності k знайдемо з таких міркувань. Оскільки ймовірність попадання точки на відрізок 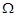є вірогідна подія, то

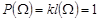, звідки .

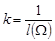Остаточно

.

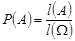Нехай простір елементарних подій W інтерпретується як область на числовій осі (на площині або у просторі), яка має відповідно довжину (площу або об’єм). Припустимо, що попадання в кожну точку цієї множини однаково можливе. Розглянемо 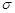- алгебру 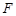всіх підмножин 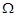, які мають довжину (відповідно площу або об’єм). Нехай подія 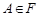. Тоді

P(А) = 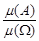, (3.1)

де m(А) – довжина (площа, об’єм) області А; m(W) – довжина (площа, об’єм) області W.

Означення 3.1. Імовірності, які обчислюються за формулою (3.1), називаються геометричними ймовірностями.

Легко перевірити, що геометричні ймовірності мають властивості аналогічні класичним ймовірностям. Зробіть це самостійно.

Приклад 3.1. На відрізку прямої 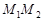, довжина якого дорівнює 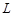, навмання обирається точка 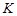. Знайти ймовірність того, що відстань від точки 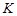до точки 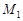більше відстані до точки .

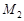Розв’язання. Позначимо через 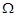множину точок відрізку 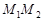, а через 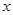– координату будь-якої точки відрізку 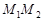, вважаючи точку 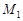початком відліку. Тоді випадковій події А={відстань від точки 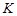до точки 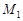більше відстані до точки 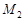} відповідає така множина точок на відрізку 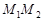: 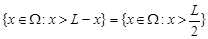. За формулою (3.1)

.

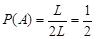Парадокс Бертрана.

В схемі геометричних ймовірностей вибір математичної моделі, яка описує реальний стохастичний експеримент, іноді буває достатньо важким. Так, якщо брати різні моделі для описання однієї події, можна отримати різні ймовірності. Продемонструємо це на прикладі.

Приклад 3.2. Парадокс Бертрана. У колі радіусом 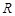обирається довільна хорда. Знайти ймовірність того, що її довжина більша, ніж довжина сторони правильного вписаного у це коло трикутника (подія 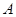). Ж. Бертран запропонував три способи розв’язання цієї задачі.

Розв’язання 1. Згідно симетрії обирається якийсь фіксований діаметр кола і розглядають всі перпендикулярні до нього хорди. Серед них і обирається навмання довільна хорда. Очевидно, що кожна хорда у цьому випадку може бути однозначно визначена своєю серединою, тобто кожній хорді можна взаємно однозначно поставити координату її середини, якщо за початок відліку взяти якийсь із кінців фіксованого діаметру. Таким чином, множина всіх значень координат середин всіх хорд – всі точки фіксованого діаметру – це множина 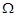. Множина, що відповідає випадковій події 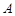, – це частина фіксованого діаметру, симетрична відносно центра кола, довжина якого дорівнює радіусу. Якщо в якості міри розглянути довжину 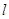, тоді за формулою (3.1)

.

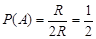Розв’язання 2. В цьому способі пропонується розглядати тільки хорди із одним закріпленим кінцем. Кожній хорді поставимо у відповідність ту частину дуги кола, яка попадає в кут 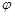. За кут 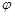позначаємо кут, що утворює хорда з дотичною, проведеною у точку закріплення одного кінця всіх хорд. Тоді множина 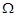–це всі точки кола, які попадають у кут 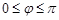, а множина 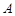–це точки кола, які попадають у кут 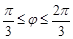. Якщо в цьому випадку за міру взяти довжину, тоді за формулою (3.1)

.

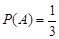Розв’язання 3. Розглядають всі хорди кола. Кожній з них взаємно однозначно ставиться точка її середини 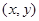, якщо за початок координат прийняти центр кола. Нехай 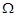– множина всіх точок, що попадають у коло радіусом 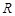, а А – множина всіх точок, які попадають у коло радіусом 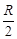. В якості міри візьмемо площу. Тоді

.

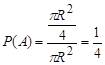Ж. Бертран був противником геометричного означення ймовірності випадкової події. Він казав, що це означення не дає можливості однозначно обчислити ймовірність однієї і тієї ж випадкової події і саме вищенаведений приклад використовував для доведення своєї правоти. Дійсно, було отримано три різних відповіді при розв’язанні одного і того ж прикладу, помилок при обчисленні не було. Так в чому ж справа? Геометричне означення ймовірності є недосконалим, чи є якась помилка у міркуваннях? Помилка полягає у різних трактуваннях поняття “навмання обрана хорда”. В кожному з трьох способів пропонувалось інше трактування цього поняття, що привело до трьох різних відповідей, тобто кожен раз розв’язувалась інша задача.

Незважаючи на певні труднощі з вибором імовірнісної моделі задачі, схема геометричних ймовірностей успішно застосовується в багатьох задачах астрономії, ядерної фізики, біології тощо.