Деякі класичні приклади обчислення геометричної імовірності випадкової події
Розглянемо деякі класичні задачі на обчислення геометричних ймовірностей випадкових подій.
Приклад 3.3. Задача про зустріч. Дві групи туристів А і В мають переправитися через річку по одній і тій же переправі. Групи підходять до переправи незалежно одна від одної протягом двох годин. Групі А для переправи потрібно 30 хв, а групі В – 15 хв. Яка ймовірність того, що жодна з груп не буде чекати переправи?
Розв’язання.
 |
Рис. 3.1
Нехай х та у – час прибуття (у годинах) кожної групи на переправу. Очевидно, що W = {(х,у): 0 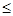 х
х 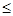 2, 0
2, 0 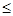 у
у 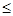 2}. Група А не буде чекати переправи, якщо
2}. Група А не буде чекати переправи, якщо 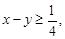 а група В – якщо
а група В – якщо 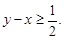 Тоді область, яка заштрихована на рис. 3.1, буде складатися з тих моментів часу прибуття груп на переправу, коли вони можуть починати переправу без чекання. За формулою геометричної ймовірності (3.1) знаходимо:
Тоді область, яка заштрихована на рис. 3.1, буде складатися з тих моментів часу прибуття груп на переправу, коли вони можуть починати переправу без чекання. За формулою геометричної ймовірності (3.1) знаходимо:
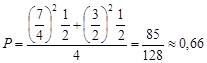 .
.
Приклад 3.4. Задача Буфона. Нехай площину розділено паралельними прямими, відстань між якими дорівнює 2а. На цю площину навмання кидають голку, довжиною 2 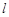 (
( 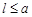 ). Знайти ймовірність того, що голка перетне яку-небудь з паралельних прямих.
). Знайти ймовірність того, що голка перетне яку-небудь з паралельних прямих.
Розв’язання. Нема сенсу розглядати всю площину, бо насправді має значення положення голки тільки відносно двох паралельних прямих. Визначимо положення голки відносно цих паралельних ліній двома параметрами (рис.3.2): відстанню 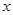 від середини
від середини 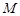 голки
голки 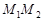 до найближчої з прямих та кутом
до найближчої з прямих та кутом 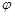 між голкою
між голкою 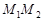 і прямою. Множина точок (
і прямою. Множина точок ( 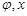 ) з можливими значеннями координат визначить множину
) з можливими значеннями координат визначить множину 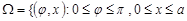 }.
}.
 | |||
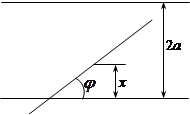 | |||
Рис. 3.2 Рис. 3.3
Голка перетне найближчу пряму тоді, коли 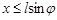 . Отже, подію А={голка перетне яку-небудь пряму} можна задати геометрично:
. Отже, подію А={голка перетне яку-небудь пряму} можна задати геометрично: 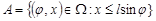 . На рис. 3.3. ця область заштрихована. Площа прямокутника
. На рис. 3.3. ця область заштрихована. Площа прямокутника 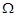 дорівнює
дорівнює 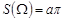 . Площу області А знайдемо так:
. Площу області А знайдемо так:
 .
.
Остаточно за формулою (3.1) маємо
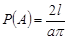 .
.
Ця задача дала можливість отримати ще одним експериментальним шляхом наближеного значення числа 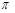 . Припустимо, що в задачі Буфона голка кидалась n разів і m разів вона перетнула яку-небудь пряму. Тоді статистична ймовірність події А буде дорівнювати
. Припустимо, що в задачі Буфона голка кидалась n разів і m разів вона перетнула яку-небудь пряму. Тоді статистична ймовірність події А буде дорівнювати 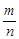 . Отже,
. Отже, 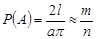 . Звідки
. Звідки
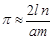 .
.
Так в літературі наведено такий приклад. Якщо 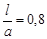 ,
, 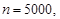
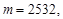 то
то 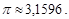
Дата добавления: 2016-11-02; просмотров: 945;
