Властивості ймовірності, що випливають з аксіом

З наведених аксіом випливають такі властивості ймовірності. (Порівняйте з властивостями класичної ймовірності, яка введена в лекції 2).

1. Якщо події утворюють повну групу подій стохастичного експерименту, то .

Ця властивість випливає з аксіом А2, А3.

2. Якщо – протилежна подія до події А, то .

Доведення. Події А і утворюють повну групу стохастичного експерименту, тому

, звідки .

3. Імовірність неможливої події дорівнює нулю: .

Це випливає з властивості 2. Зауважимо, що обернене твердження, взагалі кажучи, не є справедливим.

4. Якщо , то .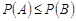

Доведення. Якщо , то подію B можна записати як об’єднання двох несумісних подій: B=A (B \ A). За аксіомою А3

.

Звідси маємо такі властивості ймовірностей:

5. Якщо , то .

6. Для : .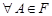

Дійсно, будь-яка випадкова подія 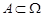, отже, .

7. Для : .

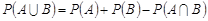Цю властивість називають теоремою додавання ймовірностей.

Доведення. Об’єднання подій представимо у вигляді об’єднання трьох попарно несумісних подій:

.

Тоді за аксіомою А3 і властивістю 5 маємо

=

= .

Теорема додавання узагальнюється так.

8. Нехай – випадкові події, тоді

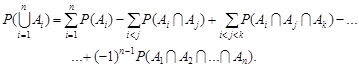
Цю властивість можна довести методом математичної індукції з властивості 7.

9. Для будь-якого скінченого або зліченного числа випадкових подій мають місце такі співвідношення:

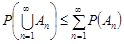і .

Доведення. Введемо послідовність випадкових подій:

, , , ...,

.

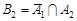Події В₁, В₂, ... , В_n,... – попарно несумісн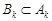і, і 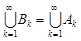. Тому

.

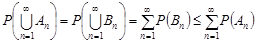Друга нерівність випливає з таких міркувань:

.

4.3. Деякі приклади застосування властивостей імовірності

Наведемо деякі приклади застосування наведених властивостей.

Приклад 4.3. Дехто має у гаманці десять банкнот по 2 грн і 5 по 5 грн. Навмання виймається 7 банкнот. Знайти ймовірність того (подія ), що загальна сума не перевищить 25 грн.

Розв’язання. Для того, щоб загальна сума не перевищувала 25 грн, треба, щоб відбулася подія = 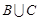, де подія В={витягнули п’ять банкнот по 2 грн і дві по 5 грн}, а подія С={витягнули чотири банкноти по 2 грн і три по 5 грн}. Події В і С – несумісні події, тоді за аксіомою Р3

.

Приклад 4.4. Задача про розсилку листів. Дехто написав листів та підписав на конвертах адреси. Потім навмання розклав листи до конвертів і заклеїв їх. Знайти ймовірність того (подія ), що принаймні один лист надійде за призначенням.

Розв’язання. Позначимо через 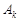випадкову подію, що полягає в тому, що - тий лист надійде за призначенням. Події 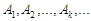– сумісні події, випадкова подія . Для знаходження ймовірності події А треба використати властивість 8. Але перш за все обчислимо .

За формулою знаходження класичної ймовірності (2.1)

Отж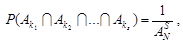е, де – число розміщень із елементів по . Тоді за властивістю ймовірності 8

Звідки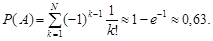

Приклад 4.5. Маємо 6 олівців різного кольору і 6 футлярів до них тих же самих кольорів. Олівці навмання розкладають по футлярах. Знайти ймовірність того, що кожен із них не буде знаходитись у своєму футлярі (подія А).

Розв’язання. Скористаємось задачею про розсилку листів і обчислимо спочатку ймовірність протилежної до А події ={принаймні один олівець буде в своєму футлярі}.

.

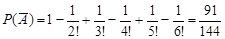За властивістю 3 ймовірності

.