Система аксіом теорії ймовірностей

Кожна з розглянутих імовірнісних схем: класична, статистична, геометрична, мають свої недоліки і не дають можливості описати всі різноманітні стохастичні експерименти. Сучасна теорія ймовірностей побудована на основі системи аксіом, які були запропоновані академіком А. М. Колмогоровим у 1929 році. Вищеназвані схеми вкладаються в цю систему як її окремі випадки.

Нехай 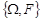– вимірний простір стохастичного експерименту, тобто виконуються умови А1, А2, А3 (лекція 1). Припустимо, що кожній події 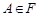поставлено у відповідність число P(А), що задовольняє умови:

Р1. " 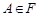: P(А)³0;

Р2. P(W) = 1 (аксіома нормування);

Р3. " А₁, А₂, ... , А_n, ...ÎF, таких, що А_iA_j=Æ, i¹j;

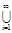P( A_i)= 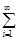P(А_i) (аксіома зчисленної адитивності).

Для розв’язання деяких задач достатньо використання аксіоми скінченої адитивності: " А₁, А₂, ... , А_nÎF, таких, що А_iA_j=Æ, i¹j справедливо співвідношення P( 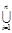A_i)= P(А_i).

Число Р(А) називається ймовірністю події А.

Твердження А1, А2, А3, Р1, Р2, Р3 складають систему аксіом теорії ймовірностей.

Так введена ймовірність події дає можливість дати строге математичне означення.

Означення 4.1. Імовірністю події 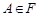називається нормована міра, яка введена на 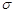- алгебрі 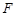простору елементарних подій .

Означення 4.2. Вимірний простір , на якому введена ймовірність, називається ймовірнісним простором.

Побудувати ймовірнісну модель експерименту означає поставити йому у відповідність імовірнісний простір 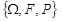. Наведемо приклади побудови деяких імовірнісних моделей експериментів.

Приклад 4.1. Стохастичний експеримент полягає в киданні монети до першої появи герба. Введемо елементарні події ={герб випав при k-му киданні монети}. Простір елементарних подій цього стохастичного експерименту буде нескінченною зліченною множиною: 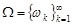. За 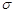- алгебри 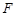візьмемо множину всіх підмножин простору . Кожній елементарній події поставимо у відповідність додатне число 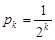. Якщо 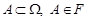, то покладемо . Тоді всі твердження А1, А2, А3, Р1, Р2, Р3 виконуються. (Перевірте самостійно!) Отже, побудований імовірнісний простір 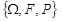є ймовірнісною моделлю відповідного стохастичного експерименту.

Приклад 4.2. Стохастичний експеримент полягає в тому, що в квадрат 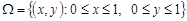навмання ставлять точку, причому попадання точки в будь-яку точку квадрата є рівноможливі події. За простір елементарних подій візьмемо квадрат , 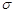- алгебра 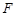включає всі підмножини квадрата, для яких має зміст поняття площі. Імовірність події 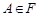введемо так: . Перевірте, що системи аксіом для так побудованої моделі цього стохастичного експерименту виконуються.

Наведені приклади показують, що система аксіом Колмогорова не суперечна, бо існують реальні стохастичні експерименти, які задовольняють цим аксіомам.

Дата добавления: 2016-11-02; просмотров: 764;