Класичне означення ймовірності випадкових подій
Нехай простір W складається із скінченого числа однаково можливих елементарних подій, тобто W={w1, w2, ... , wn}. Однаково можливими вважають такі елементарні події, якщо нема сенсу припускати, що якась із подій буде відбуватися частіше за інші. Наприклад, якщо гральний кубик зроблено з однорідної речовини та витримана повна симетрія його граней, то при киданні кубика, він з однаковою можливістю може впасти на будь-яку з шести граней.
Внаслідок однакової можливості появи кожної елементарної події 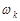 логічно вважати, що
логічно вважати, що
P(w1) = P(w2) = ... = P(wn) = 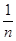 .
.
Нехай  . Тоді
. Тоді
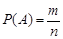 , (2.1)
, (2.1)
де  – число елементарних подій, які сприяють появі події
– число елементарних подій, які сприяють появі події  ;
; 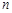 – число всіх елементарних подій.
– число всіх елементарних подій.
Означення 2.1. Імовірність випадкової події, яка обчислюється за формулою (2.1), називається класичною ймовірністю.
Зауважимо, що для класичної ймовірності справедливі всі властивості 1) – 8).
Приклад 2.1. Задача провибір. Нехай є 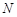 деталей, серед яких –
деталей, серед яких – 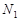 деталей першого сорту,
деталей першого сорту,  деталей – другого сорту,
деталей – другого сорту, 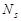 деталей –
деталей – 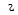 - того сорту, тобто
- того сорту, тобто  . Із всієї партії навмання відбирають
. Із всієї партії навмання відбирають 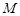 деталей. Обчислити ймовірність того (подія
деталей. Обчислити ймовірність того (подія  ), що серед відібраних
), що серед відібраних 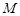 деталей
деталей  – першого сорту,
– першого сорту,  – другого сорту, ... ,
– другого сорту, ... , 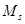 –
– 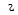 - того сорту, тобто
- того сорту, тобто  .
.
Розв’язання. Скористаємось класичним означенням ймовірності. Число всіх результатів експерименту дорівнює  , число елементарних подій, які сприяють появі події
, число елементарних подій, які сприяють появі події  дорівнює
дорівнює 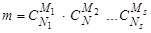 . Отже, ймовірність випадкової події
. Отже, ймовірність випадкової події  , яка обчислюється за формулою (2.1), дорівнює
, яка обчислюється за формулою (2.1), дорівнює

Приклад 2.2. На 20 каналів зв’язку надходить 30 телеграм. Прибуття кожної з них на кожному каналі однаково можливе. Обчислити ймовірність того, що на один із каналів надійде 10 телеграм, на другий – дві, а всі інші розподіляться по різних каналах (подія  ).
).
Розв’язання. Кількість елементарних подій стохастичного експерименту, який розглядається в задачі, дорівнює  , бо кожна телеграма може розміститися на каналах зв’язку двадцятьма способами. Кількість елементарних подій, які сприяють появі події
, бо кожна телеграма може розміститися на каналах зв’язку двадцятьма способами. Кількість елементарних подій, які сприяють появі події  дорівнює
дорівнює 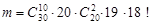 Дійсно, кількість способів, якими обираються 10 телеграм із 30, без урахування порядку, дорівнює
Дійсно, кількість способів, якими обираються 10 телеграм із 30, без урахування порядку, дорівнює  ; кількість способів, якими обирається якийсь канал з 20 каналів, дорівнює 20; кількість способів, якими обираються 2 телеграми з 20, що залишилися, без урахування порядку, дорівнює
; кількість способів, якими обирається якийсь канал з 20 каналів, дорівнює 20; кількість способів, якими обираються 2 телеграми з 20, що залишилися, без урахування порядку, дорівнює  ; кількість способів, якими обирається один із 19 каналів, дорівнює 19; 18 телеграм, що залишились, розподіляються по 18 каналах (з урахуванням порядку) 18! способами. Отже, ймовірність випадкової події
; кількість способів, якими обирається один із 19 каналів, дорівнює 19; 18 телеграм, що залишились, розподіляються по 18 каналах (з урахуванням порядку) 18! способами. Отже, ймовірність випадкової події  , яка обчислюється за формулою (2.1), дорівнює
, яка обчислюється за формулою (2.1), дорівнює
 .
.
Приклад 2.3. Десятеро пасажирів входять до ліфта шістнадцятиповерхового будинку. Кожен із них має однакову можливість вийти на будь-якому поверсі, починаючи з другого. Знайти ймовірність того, що 3 пасажири вийдуть на п’ятому поверсі, 4 – на одному із поверхів між шостим та десятим поверхами, а останні вийдуть на шістнадцятому поверсі (подія  ).
).
Розв’язання. Задача розв’язується за тією ж схемою, що попередня (поверхи – канали зв’язку, пасажири – телеграми). Тому кількість можливих результатів стохастичного експерименту в цій задачі дорівнює  . Кількість результатів, які сприяють появі випадкової події
. Кількість результатів, які сприяють появі випадкової події  , дорівнює
, дорівнює 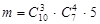 , тобто спочатку обираємо трьох пасажирів із десяти, не враховуючи порядок, які вийдуть на п’ятому поверсі (способів такого вибору буде
, тобто спочатку обираємо трьох пасажирів із десяти, не враховуючи порядок, які вийдуть на п’ятому поверсі (способів такого вибору буде  ). Поверх вже визначено, тому він обирається одним способом. Далі обираємо чотирьох пасажирів із семи, що залишилися, без урахування порядку (способів такого вибору буде
). Поверх вже визначено, тому він обирається одним способом. Далі обираємо чотирьох пасажирів із семи, що залишилися, без урахування порядку (способів такого вибору буде  ) і поверх, на якому вони вийдуть (способів такого вибору – 5 ). Останні троє пасажирів вийдуть на останньому поверсі одним способом. Таким чином
) і поверх, на якому вони вийдуть (способів такого вибору – 5 ). Останні троє пасажирів вийдуть на останньому поверсі одним способом. Таким чином
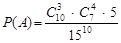 .
.
Приклад 2.4. На полиці розташовано 20 книг. Їх перемішують і розставляють у довільному порядку. Знайти ймовірність того, що три певних із цих книжок стоятимуть поряд (подія  ).
).
Розв’язання. Кількість елементарних подій цього стохастичного експерименту дорівнює 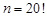 Для того, щоб обчислити кількість елементарних подій, які сприяють появі події
Для того, щоб обчислити кількість елементарних подій, які сприяють появі події  , уявімо книжки, які нас цікавлять, зв’язаними разом. Тоді всіх книжок буде 18 і серед них одна товста, що складається з трьох книжок. Ці 18 книжок можна переставляти 18! способами. Але три книжки, що зв’язані в одну товсту, можна зв’язати 3! способами. Таким чином, число сприятливих події
, уявімо книжки, які нас цікавлять, зв’язаними разом. Тоді всіх книжок буде 18 і серед них одна товста, що складається з трьох книжок. Ці 18 книжок можна переставляти 18! способами. Але три книжки, що зв’язані в одну товсту, можна зв’язати 3! способами. Таким чином, число сприятливих події  результатів дорівнює
результатів дорівнює 
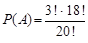 .
.
Дата добавления: 2016-11-02; просмотров: 1333;
