Міра вірогідності випадкових подій
Якщо стохастичний експеримент повторювати неодноразово, то можна помітити, що деякі випадкові події з’являються частіше за інших. Щоб якось порівнювати випадкові події з цієї точки зору, треба ввести кількісну міру їх вірогідності, тобто таку кількісну характеристику випадкової події, згідно з якою можна було б казати, що одна випадкова подія більш вірогідна, ніж інша. Цю міру в подальшому називатимемо ймовірністю випадкової події. На жаль не можна навести єдиного означення ймовірності до всіх випадкових подій.
Розглянемо такі стохастичні експерименти, які можна задавати скінченим простором елементарних подій  . Нехай W={w1, w2, ..., wn}. Алгебра
. Нехай W={w1, w2, ..., wn}. Алгебра 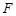 – це множина всіх підмножин простору
– це множина всіх підмножин простору  . Поставимо у відповідність кожному
. Поставимо у відповідність кожному 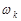 деяке число pk
деяке число pk 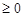 так, щоб
так, щоб 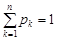 і назвемо його ймовірністю елементарної події
і назвемо його ймовірністю елементарної події 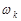 . Нехай А – випадкова подія стохастичного експерименту, тобто
. Нехай А – випадкова подія стохастичного експерименту, тобто 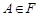 . Це означає, що
. Це означає, що  ,
, 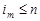 . Подія А відбулася, якщо відбулася принаймні одна з елементарних подій wÎА. За ймовірність появи події А доречно взяти величину
. Подія А відбулася, якщо відбулася принаймні одна з елементарних подій wÎА. За ймовірність появи події А доречно взяти величину 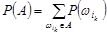 . Означена таким способом імовірність появи події А має такі властивості:
. Означена таким способом імовірність появи події А має такі властивості:
1) " АÎF: 0 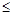 P(А) £ 1;
P(А) £ 1;
2) P(  ) = 1;
) = 1;
3) P( 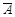 ) = 1 – P(А);
) = 1 – P(А);
4) P(Æ) = 0;
5) P(А 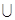 В) = P(А)+P(В) – P(А
В) = P(А)+P(В) – P(А 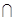 В)
В)
(теорема додавання ймовірностей);
6) зокрема для несумісних подій P(А 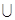 В) = P(А)+P(В);
В) = P(А)+P(В);
7) якщо А Ì В, то P(А) £ P(В),
8) якщо 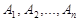 – повна група подій стохастичного експерименту, то
– повна група подій стохастичного експерименту, то 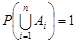 .
.
Дата добавления: 2016-11-02; просмотров: 591;
