Незалежність випадкових подій

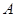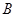Означення 6.2. Випадкові події та називаються незалежними, якщо виконується одна з рівностей

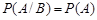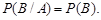або (6.5)

Рівності (6.5) означають, що на появу однієї події не впливає поява другої події.

В прикладних задачах для визначення незалежності двох випадкових подій часто користуються інтуїтивними міркуваннями або міркуваннями, які основані на досліді.

Розглянемо деякі властивості незалежності подій.

1. Справедлива теорема множення для двох незалежних подій: якщо випадкові події А та В – незалежні, то

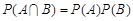. (6.6)

Формула (6.6) є наслідком означення 6.2 та формули (6.3).

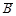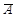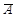2. Якщо випадкові події А та В – незалежні, то події А і , і В, і 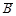також будуть незалежними випадковими подіями.

Доведення. Доведемо, наприклад, що з незалежності випадкових подій А і В випливає незалежність подій А і 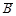. Дійсно, 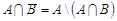. Отже,

.

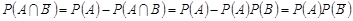3. Якщо випадкові події А і В та А і С – незалежні події, а події В і С – несумісні події, то події А і 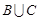будуть незалежними випадковими подіями.

Проведіть доведення самостійно.

Узагальнимо поняття незалежності на сукупність n подій.