Статистична ймовірність випадкових подій
Тривалі спостереження над появою чи не появою випадкової події  при дотриманні одного і того ж комплексу умов показують, що для широкого кола подій кількість появ чи не появ підкоряється стійким закономірностям. А саме, якщо ми за
при дотриманні одного і того ж комплексу умов показують, що для широкого кола подій кількість появ чи не появ підкоряється стійким закономірностям. А саме, якщо ми за 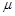 позначимо кількість появ події
позначимо кількість появ події  при
при 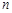 незалежних випробуваннях, то виявляється, що відношення
незалежних випробуваннях, то виявляється, що відношення 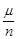 для достатньо великих
для достатньо великих 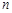 у більшості таких серій спостережень зберігає майже постійну величину. Назвемо відношення
у більшості таких серій спостережень зберігає майже постійну величину. Назвемо відношення 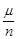 відносною частотою появи події А. Вперше стійкість частот було виявлено на явищах демографічного характеру. Так вже в давнину було помічено, що для цілих держав і великих міст відношення кількості новонароджених хлопчиків до кількості всіх новонароджених із року в рік залишається майже незмінним. В старому Китаї задовго до нашої ери це число вважалось рівним 0,5. Пізніше, особливо у 17 та 18 сторіччях з’явився ряд фундаментальних праць, присвячених вивченню статистики народонаселення. Виявилось, що крім стійкості у відносному числі народжень хлопчиків та дівчаток, спостерігалися стійкі закономірності і іншого характеру: відсоток смертності у визначеному віці для визначених груп населення ( в залежності від соціальних та матеріальних умов), розподіл людей (визначеної статі, віку та національності) за зростом, довжиною ступні і т. і. У відомій книзі “Досвід філософії теорії ймовірностей” Лаплас розповів про один дуже цікавий епізод, що стався з ним при вивчені закономірностей народження хлопчиків та дівчаток. Численні статистичні матеріали, вивчені їм для Лондона, Петербурга, Берліна та всієї Франції, давали майже точно співпадаючі відношення кількості народжених хлопчиків до кількості всіх народжених. Всі ці відношення коливались протягом десятиріч біля одного і того ж числа, яке приблизно дорівнює
відносною частотою появи події А. Вперше стійкість частот було виявлено на явищах демографічного характеру. Так вже в давнину було помічено, що для цілих держав і великих міст відношення кількості новонароджених хлопчиків до кількості всіх новонароджених із року в рік залишається майже незмінним. В старому Китаї задовго до нашої ери це число вважалось рівним 0,5. Пізніше, особливо у 17 та 18 сторіччях з’явився ряд фундаментальних праць, присвячених вивченню статистики народонаселення. Виявилось, що крім стійкості у відносному числі народжень хлопчиків та дівчаток, спостерігалися стійкі закономірності і іншого характеру: відсоток смертності у визначеному віці для визначених груп населення ( в залежності від соціальних та матеріальних умов), розподіл людей (визначеної статі, віку та національності) за зростом, довжиною ступні і т. і. У відомій книзі “Досвід філософії теорії ймовірностей” Лаплас розповів про один дуже цікавий епізод, що стався з ним при вивчені закономірностей народження хлопчиків та дівчаток. Численні статистичні матеріали, вивчені їм для Лондона, Петербурга, Берліна та всієї Франції, давали майже точно співпадаючі відношення кількості народжених хлопчиків до кількості всіх народжених. Всі ці відношення коливались протягом десятиріч біля одного і того ж числа, яке приблизно дорівнює 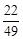 . В той же час дослідження статистичних матеріалів аналогічного характеру по Парижу за 40 років (із 1745 до 1784) приводило до іншого числа.
. В той же час дослідження статистичних матеріалів аналогічного характеру по Парижу за 40 років (із 1745 до 1784) приводило до іншого числа. 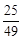 . Лапласа зацікавила ця суттєва різниця. Він почав шукати для неї раціональне пояснення. При детальному вивчені архівних матеріалів виявилося, що загальна кількість народжень по Парижу включало також всіх підкидьок. Виявилось також, що околишнє населення підкидало в основному новонароджених однієї статі, а саме дівчаток. Коли Лаплас включив до загальної кількості всіх народжених підкидьок, то відношення кількості народжених хлопчиків до кількості всіх народжених по місту Парижу співпало з аналогічним відношенням по всіх інших містах і по всій Франції в цілому.
. Лапласа зацікавила ця суттєва різниця. Він почав шукати для неї раціональне пояснення. При детальному вивчені архівних матеріалів виявилося, що загальна кількість народжень по Парижу включало також всіх підкидьок. Виявилось також, що околишнє населення підкидало в основному новонароджених однієї статі, а саме дівчаток. Коли Лаплас включив до загальної кількості всіх народжених підкидьок, то відношення кількості народжених хлопчиків до кількості всіх народжених по місту Парижу співпало з аналогічним відношенням по всіх інших містах і по всій Франції в цілому.
З часів Лапласа накопичено багато статистичних матеріалів, які дозволяють з великою впевненістю розраховувати наперед кількісні характеристики суспільно важливих демографічних явищ. Той факт, що при великій кількості випробувань, для ряду випадкових подій відносна частота залишається майже незмінною, примушує нас припустити, що існують незалежні від дослідника закономірності протікання явищ, виявлення яких і полягає в зазначеній сталості відносної частоти. Та обставина, що для подій, до яких можна застосовувати класичне означення ймовірності, відносна частота при великій кількості випробувань, як правило, близька до ймовірності, примушує вважати в загальному випадку, що існує деяка стала, навколо якої коливається ця частота. Цю сталу, що є об’єктивною числовою характеристикою появи події, природно назвати ймовірністю випадкової події, що досліджується. Таким чином ми прийшли ще до одного означення ймовірності.
Означення 2.2. Статистичною ймовірністю випадкової події А називається число 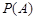 , що дорівнює відносній частоті появи цієї події при проведені серії з n експериментів, тобто
, що дорівнює відносній частоті появи цієї події при проведені серії з n експериментів, тобто
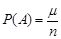 .
.
Таке означення ймовірності випадкової події інколи викликає недовіру, аргументоване тим, що відносна частота появи випадкової події може змінюватися при проведенні різних експериментів. Але коли людині пропонують виміряти довжину якогось відрізка за допомогою лінійки, ні в кого не виникає сумніву в тому, що це можна зробити. Нікого не хвилює той факт, що якщо провести теж саме вимірювання більш досконалим вимірювальним пристроєм, то можна отримати інший результат. Справа полягає в точності вимірювання. Аналогічно треба відноситись і до статистичного означення ймовірності випадкової події.
Зауважимо, що існує інша точка зору на статистичне означення ймовірності випадкової події. В деяких підручниках пропонується за статистичну ймовірність випадкової події вважати границю послідовності відносних частот, яка виникає при проведені різних серій випробувань. Але з точки зору математичного аналізу в цьому означенні є деяке непорозуміння. Воно полягає в тому, що не можна отримати всі члени послідовності відносних частот, тобто не можна задати правила, за яким отримується довільний член цієї послідовності. Це означає, що не можна визначити границю послідовності, яку неможливо побудувати.
З означення 2.2. випливають такі властивості статистичної ймовірності:
1) 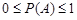 ;
;
2) 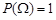 ;
; 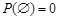 ;
;
3) якщо 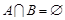 ,то
,то 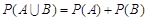 .
.
Дата добавления: 2016-11-02; просмотров: 1189;
