Коефіцієнт запасу та ймовірності досягнення граничного стану
Чинні норми проектування мостів мають детерміністичний характер. В розрахунках засобом недопущення граничного стану є коефіцієнт надійності. Його природу нескладно показати аналітично, якщо вважати, що розподіл опору R та навантаження Q є нормальними і між ними відсутній кореляційний зв'язок [19].
Згідно з роботою А.Р.Ржаніцина, введено узагальнений коефіцієнт запасу – математичне сподівання
 , (5.1)
, (5.1)
та розрахунковий коефіцієнт
 . (5.2)
. (5.2)
Для кожного із розподілів може бути встановлений зв'язок між коефіцієнтами – показниками безпеки γ0 і γk та ймовірністю досягнення граничного стану. Так для випадку, коли R і Q описуються нормальним розподілом, отримано:
 . (5.3)
. (5.3)
Чисельник і знаменник цієї залежності розділино на μk
 . (5.4)
. (5.4)
Залежність між узагальненим коефіцієнтом запасу γ0 та характеристикою безпеки β має вигляд
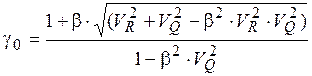 . (5.5)
. (5.5)
Після внесення в (5.2) статистично модельовані значення узагальненого опору Rk та Qk, отримано
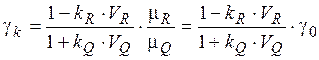 . (5.6)
. (5.6)
Тут, як і раніше, VRі VQ - коефіцієнти варіації випадкових змінних R та Q відповідно; kRі kQ - їх коефіцієнти забезпеченості.
Таким чином, співвідношеннями (5.3, 5.4) встановлюється залежність між коефіцієнтами запасу γ0і γk, ймовірнісними характеристиками узагальнених опору та навантаження і ймовірністю досягнення граничного стану.
Для практичних застосувань є зручною формула, що витікає із співвідношення (5.3), якою зв’язується характеристика безпеки з математичним сподіванням узагальненого коефіцієнта запасу та коефіцієнтами варіації опору та навантаження

 . (5.7)
. (5.7)
5.3 Проектування елементів мостів за критерієм надійності
Ймовірнісні розрахунки за критерієм надійності мають за мету пошук оптимального проекту при заданому рівні безпеки. За критерій приймається характеристика безпеки β.
Ймовірнісні розрахунки за критерієм надійності мають виконуватись так, щоби фундаментальна нерівність методу граничних станів, якій має задовольняти елемент, що проектується, зоставалась непорушною:
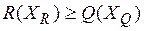 , (5.8)
, (5.8)
де R(XR)– функція опору елемента;
Q(XQ)– функція зовнішніх навантажень елемента;
XR – базові змінні, якими виражається несуча здатність елемента;
XQ - базові змінні, якими виражається зовнішнє навантаження елемента.
Стверджується, що базові змінні, якими виражається несуча здатність і зовнішнє навантаження елемента, мають нормальний чи логнормальний розподіл.
Базові змінні Xі в (5.8) визначаються через параметри закону розподілу, прийнятого для змінної:
 , (5.9)
, (5.9)
де μі – математичне сподівання базової змінної;
αі – координата проектної точки базової змінної;
σі – стандарт базової змінної, згідно з законом розподілу;
β – прийнята характеристика безпеки;
Vі – коефіцієнт варіації базової змінної.
Для розрахунків знадобляться нормативні значення характеристики безпеки b. Рекомендується до прийняття відповідного нормативного документа застосовувати значення β, які наведені в таблиці 5.1.
Таблиця 5.1 – Рекомендовані мінімальні значення характеристики безпеки
| Вид розрахунків | Характеристика безпеки |
| Розрахунок міцності | 3,8 |
Продовження таблиці 5.1
| Розрахунок локальної міцності | 3,0 |
| Розрахунок витривалості | 2,0 |
| Розрахунок деформацій | 1,64 |
| Розрахунки поздовжнього тріщиноутворення | 1,64 |
| Розрахунки поперечного тріщиноутворення | 1,28 |
Iмовірнісна модель проектування елементів, виражена через статистичні параметри опору та навантаження, - аналог фундаментальної нерівності методу граничних станів, має вигляд:
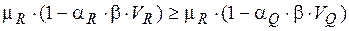 . (5.10)
. (5.10)
де μR та μQ – математичні сподівання узагальненого опору та навантаження, відповідно;
αR та αQ – координати проектної точки узагальненого опору та навантаження, відповідно;
σR та σQ – стандарти базової змінної, згідно з законом розподілу;
β – прийнята характеристика безпеки;
VR та VQ – коефіцієнти варіації узагальненого опору та навантаження, відповідно.
Для елемента, який проектується, необхідно перевіряти виконання нерівності
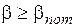 , (5.11)
, (5.11)
де βпот – приписане нормативним документом мінімальне значення характеристики безпеки (табл. 5.7);
β – значення характеристики безпеки, обчислене відносно запроектованого елемента, за виразом

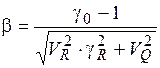 . (5.12)
. (5.12)
Математичні сподівання узагальненого опору та навантаження, які відповідають коефіцієнтам рівня довіри VR = 0.95та VQ = 0.95знаходяться за формулами:
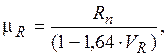 (5.13)
(5.13)
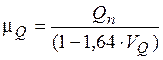 , (5.14)
, (5.14)
де Rn та Qn – нормативні значення опору (несучої здатності) та навантаження елемента відповідно.
Необхідні для обчислень коефіцієнти варіації рухомих та постійних навантажень наведені в таблицях 5.2-5.6.
Таблиця 5.2 – Коефіцієнти варіації VQ тимчасових рухомих навантажень АК
| Тип навантаження | Випадок застосування | Коефіцієнт варіації, VQ |
| Тандем навантаження АК | В розрахунках елементів проїзної частини мостів | 0,17 |
| В розрахунках всіх інших елементів мостів | 0,17 при λ < 30 м 0,07 при λ ≥ 30м | |
| Рівномірно-розповсюджене навантаження АК | У всіх розрахунках конст-рукцій мостів на вертикальні і горизонтальні дії від рухомого навантаження | 0,24 |
Примітка: λ – довжина лінії впливу.
Таблиця 5.3 – Коефіцієнт варіації VQ постійних навантажень і впливів
| Навантаження і впливи | Позначення фактора | Коефіцієнти варіації, VQ |
| Власна вага | gt | 0,033 |
| Площа поперечного перерізу елемента | Ared | 0,0237 |
| Момент опору поперечного перерізу елемента | Wred | 0,0229 |
| Ексцентриситет точки фіксації сили попереднього напруження | en | 0,0167 |
| Навантаження ваги проїзної частини і тротуарів автодорожніх мостів | g2 | 0,170 |
| Вплив повзучості бетону | g3 | 0,030 |
Таблиця 5.4 - Коефіцієнт варіації VR геометричних характеристик поперечного перерізу елемента
| Геометричні характеристики | Позначення фактора | Коефіцієнти варіації, VQ |
| Площа поперечного перерізу елемента | Ared | 0,0237 |
| Момент опору поперечного перерізу елемента | Wred | 0,0229 |
Таблиця 5.5 – Коефіцієнт варіації VR арматури залізобетонних елементів
| Клас арматури | A-I | A-II | A-III | A-IV | A-V | A-VI | Ат-III |
| Коефіцієнт варіації, VR | 0,07 | 0,07 | 0,07 | 0,09 | 0,09 | 0,04 | 0,11 |
| Клас арматури | Aт-IV | Aт-IV | Aт-IV | A-IIIв | Дріт холодного витягу | Канати | |
| Коефіцієнт варіації, VR | 0,08 | 0,07 | 0,08 | 0,06 | 0,08 | 0,05 |
Таблиця 5.6 – Коефіцієнт варіації VR міцності бетону
| Vb,28, МПа | ||||||||
| За умови натураль-ного твердіння | 0,159 | 0,129 | 0,105 | 0,082 | 0,066 | 0,054 | 0,051 | 0,051 |
| За умови теплової обробки | 0,121 | 0,111 | 0,094 | 0,090 | 0,078 | 0,066 | 0,055 | 0,052 |
Дата добавления: 2016-09-20; просмотров: 775;
